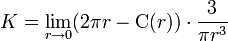Lo que hizo Nepper es un ejemplo de geometría no-euclidianas (más particularmente: geometría esférica), donde el único "error" fué considerar que PI sería una constante, cuando en realidad será un valor entre 3.14.. y 0 según lo "grande" que sea el radio del círculo (como ya comentó Alejandro)
Creo que vos no estás teniendo en cuenta que los "círculos" y los "radios" de que se está hablando no son los "tradicionales", sino que son los que medirías moviéndote por la superficie.
Ejemplos de una superficie curva en el espacio son los mas comunes porque son faciles de dibujar, pero se prestan a confusión si uno lo mira desde "afuera" y quiere medir saliéndose de la superficie.
En el caso de la Tierra, el Ecuador tiene un perímetro de 40000km. El radio euclidiano de ese círculo es el radio de la Tierra. Pero en geometría esférica es 20000km, porque no podés medir bajo tierra

.
Y para agregarte otra curiosidad, acá las paralelas se cortan.
Otro caso donde PI no es una constante es en la relatividad general.
Si vos estuvieras cerca de una estrella de neutrones (o cualquier otra cosa que deforme el espacio) y trazaras un círculo alrededor de la estrella. Si medís el perímetro y el radio, te vas a encontrar que perimetro/radio es menor que 2PI.