Introducción
Al escuchar la palabra "digital", probablemente lo primero que llega a nuestra mente es "Computadora", "CD", "DVD", etc. Debido al gran alcance que han tenido todo tipo de aparatos electrónicos, en este momento son muy pocas las áreas de la vida moderna que no cuenten con un sistema digital, ya sea de medición, comparación, operaciones aritméticas o diversión.
Además de que, al desplazar muchos de los circuitos "análogos", los circuitos digitales han permitido que las nuevas tecnologías estén al alcance de casi cualquier persona.
Abarcando mercados que desde su invención, eran territorio exclusivo de los sistemas análogos, y abaratando costos, así como permitiendo que los equipos sean cada vez más pequeños, livianos y que necesiten de una menos cantidad de energía para funcionar.
En este pequeño tutorial, vamos a comprender cómo funciona este mundo tan fascinante como sencillo.
¿Cómo vemos los números?
En casi todos los campos de la vida humana (por no decir todos), el concepto de "cantidades" es el más utilizado para definir, medir, contar, expresar o utilizar todo tipo de efectos físicos con los que nos encontramos en la vida diaria.
Cuando necesitamos modificar estas cantidades, es primordial que podamos representar estas cantidades de manera exacta y sencilla, para ese efecto, nos valemos de dos formas de representación numérica de estas cantidades.
El ejemplo clásico es un voltímetro analógico, el cuál cuenta con una aguja medidora que se mueve sobre una escala de números, el movimiento de la aguja es proporcional al voltaje que se aplique a las puntas del voltímetro. La posición de esta aguja representa el valor del voltaje que se mide, y esta sigue continuamente cualquier cambio que se presente en el mismo.
Las cantidades analógicas muestran una característica que hay que destacar, pueden variar gradualmente dentro de una línea continua de valores. El voltaje aplicado al voltímetro puede ser de cualquier valor comprendido entre los de 0 a 12 volts (suponiendo que esa fuera su escala), algo como 1.25V o 10.59V.
En la representación Digital estas mismas cantidades no se presentan con valores continuos, en cambio, se presentan como símbolos, que llamaremos Dígitos, por ejemplo.
El mismo voltímetro digital, (que cuenta con dos dígitos), no podría medir los voltajes intermedios que existen entre las unidades. Por ejemplo, si inicialmente tengo un valor de 1V, el display del voltímetro me mostraría 01 V, si yo aumento este valor hasta 1.7V, me mostraría 1V. Sólo puede cambiar hasta que el voltaje de entrada rebasara los 2V. En este caso el cambio no es continuo, cada cambio en el dígito del display, representa 1 voltio.
¿Cómo diferenciar un valor Analógico de uno Digital?
La diferencia más obvia entre un valor Analógico y otro Digital se puede determinar fácilmente de la siguiente manera:
Los valores Digitales, no dejan espacio a dudas ni interpretaciones, ya que su cantidad puede estar dentro de un amplio rango de medidas, pero tiene un solo valor.
Ventajas de los sistemas Digitales.
Cada vez aumenta más el número de usos en el campo de la electrónica (y en muchos otros campos) para los sistemas digitales, en los cuáles reinaban los sistemas análogos. Muchas son las razones para este cambio, algunas de las más importantes son:
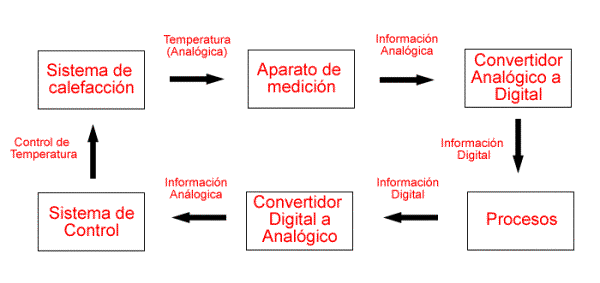
Podemos lograr que un circuito digital haga lo cualquier cosa que necesitemos dentro de los parámetros del mundo digital, pero, ¿Cómo podemos hacer para que este circuito "comprenda" todos los valores de nuestro mundo, que por regla básica es completamente analógico?
Esta, es la única desventaja al utilizar sistemas digitales.
En su gran mayoría, las fuerzas físicas en el mundo real son analógicas, y los sistemas digitales las utilizan como entradas y salidas de información para efectuar las acciones que necesitemos con ellas, como medición y control.
Algunos ejemplos son:
Esta aproximación de valores un ejemplo claro de cómo podemos "traducir" los valores analógicos en valores digitales que nuestro circuito pueda interpretar y manipular sin problemas
Por consiguiente, para poder utilizar los sistemas digitales para trabajar con valores analógicos, se vuele prioridad seguir una serie de pasos, los cuáles serían:
 ¿Que son los números Digitales?
¿Que son los números Digitales?
Dentro del mundo digital, se utilizan varios sistemas de numeración, de estos, los de uso común son:
El sistema DECIMAL, está formado por diez símbolos (numerales), 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Para poder expresar una cantidad es necesario utilizar estos símbolos como dígitos de un número.
En el sistema decimal, cada número (además de su valor numeral) toma su valor dependiendo de la posición donde se encuentre colocado dentro del número.

Pongamos el ejemplo del número 1495, siguiendo la tabla arriba mencionada, sabemos que:
2.- Sistema Binario
Debido a su naturaleza analógica, el sistema decimal no es útil si la intención es diseñar un circuito digital, ya que tenemos 10 diferentes números para trabajar, lo que causaría un enorme trabajo para poder realizar hasta las tareas más sencillas.
Basados en esta complicación, al diseñar los circuitos digitales se optó por un sistema mucho más eficaz para este tipo de trabajo, La manera más fácil de trabajar sería teniendo solamente dos niveles de voltaje, dos variables. Así se llegó a la solución de utilizar el sistema BINARIO (base 2), como base principal para los circuitos digitales, aunque no exclusiva.
En el sistema Binario, los numerales toman su valor de manera posicional (como el decimal), cada dígito binario utiliza su propio valor expresado a la potencia de 2.
En este sistema, por abreviación, el Dígito Binario se nombra como BIT, Quedando la tabla para un número de 4 bits como sigue:

Resumiendo, en un número de cuatro bits, el valor de cada bit dependiendo de su posición es calculado fácilmente con la siguiente tabla:

En un número de ocho bits quedaría como:

Conteo Binario
En la siguiente tabla usaremos un número de 4 bits para crear un conteo, al inicio de al cuenta, todos los bits están en cero.
Con cada conteo, el LSB cambia su valor de un número binario al otro, cada vez que este cambia de 1 a 0, el segundo bit cambia de estado también, cuando los dos primeros bits cambian de 1 a 0, el tercer bit cambia su estado, y cuando los tres primeros bits cambian de 1 a 0, cambia el MSB.
En la siguiente tabla s e muestra el conteo Binario de un número de cuatro Bits:
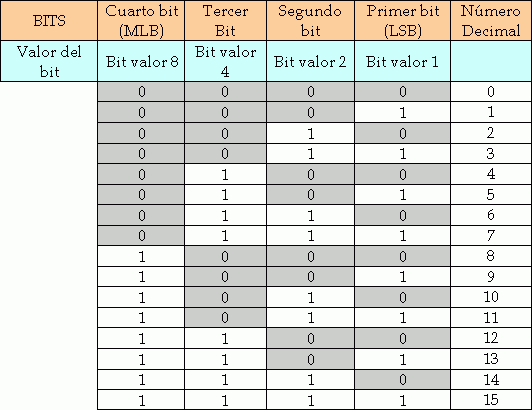
Observando con detalle la tabla anterior, se llega a la conclusión de que el conteo binario tiene una muy marcada característica:
3.- Sistema Octal
El sistema de numeración octal es también muy utilizado en los sistemas digitales, la diferencia frente al sistema Binario es que sólo puede tener ocho posibles dígitos 0, 1, 2, 3, 4, 5,6 ,7. Por lo tanto, cada Bit de un número Octal sólo puede un valor del 0 al 7.
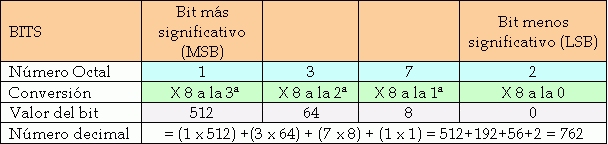
Conteo Octal
El mayor dígito del sistema Octal es el 7, por lo que cuando hacemos un conteo hacia arriba se incrementa un dígito por conteo, al llegar al número 7, se reinicia la cuenta de ese bit y al siguiente se le incrementa su conteo un dígito.
4.- Sistema Hexadecimal
El sistema de numeración hexadecimal (Hex), es parecido al sistema octal, pero con la diferencia que es base 16, por lo que puede tener hasta 16 símbolos (numerales), utilizando dígitos de la A a la F para representar los números del 10 al 15. Quedando: 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
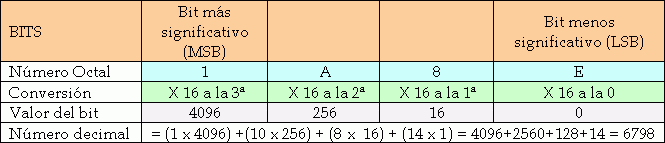
Conteo Hexadecimal
El mayor número del sistema Hexadecimal (Hex) es el 15, por lo que cuando hacemos un conteo hacia arriba se incrementa un dígito por conteo, al llegar a la F (15), se reinicia la cuenta de ese Bit y al siguiente de le incrementa su conteo un dígito:
Primer conteo = 28, 29, 2A, 2B, 2C, 2D, 2E, 2F, 30, 31, 32...
Segundo conteo = 5F8, 5F9, 5FA, 5FB, 5FC, 5FD, 5FE, 5FF, 600, 601, 602...
Segunda parte: Conversiones entre códigos.
Al escuchar la palabra "digital", probablemente lo primero que llega a nuestra mente es "Computadora", "CD", "DVD", etc. Debido al gran alcance que han tenido todo tipo de aparatos electrónicos, en este momento son muy pocas las áreas de la vida moderna que no cuenten con un sistema digital, ya sea de medición, comparación, operaciones aritméticas o diversión.
Además de que, al desplazar muchos de los circuitos "análogos", los circuitos digitales han permitido que las nuevas tecnologías estén al alcance de casi cualquier persona.
Abarcando mercados que desde su invención, eran territorio exclusivo de los sistemas análogos, y abaratando costos, así como permitiendo que los equipos sean cada vez más pequeños, livianos y que necesiten de una menos cantidad de energía para funcionar.
En este pequeño tutorial, vamos a comprender cómo funciona este mundo tan fascinante como sencillo.
¿Cómo vemos los números?
En casi todos los campos de la vida humana (por no decir todos), el concepto de "cantidades" es el más utilizado para definir, medir, contar, expresar o utilizar todo tipo de efectos físicos con los que nos encontramos en la vida diaria.
Cuando necesitamos modificar estas cantidades, es primordial que podamos representar estas cantidades de manera exacta y sencilla, para ese efecto, nos valemos de dos formas de representación numérica de estas cantidades.
- La representación Analógica.
- La representación Digital.
El ejemplo clásico es un voltímetro analógico, el cuál cuenta con una aguja medidora que se mueve sobre una escala de números, el movimiento de la aguja es proporcional al voltaje que se aplique a las puntas del voltímetro. La posición de esta aguja representa el valor del voltaje que se mide, y esta sigue continuamente cualquier cambio que se presente en el mismo.
Las cantidades analógicas muestran una característica que hay que destacar, pueden variar gradualmente dentro de una línea continua de valores. El voltaje aplicado al voltímetro puede ser de cualquier valor comprendido entre los de 0 a 12 volts (suponiendo que esa fuera su escala), algo como 1.25V o 10.59V.
En la representación Digital estas mismas cantidades no se presentan con valores continuos, en cambio, se presentan como símbolos, que llamaremos Dígitos, por ejemplo.
El mismo voltímetro digital, (que cuenta con dos dígitos), no podría medir los voltajes intermedios que existen entre las unidades. Por ejemplo, si inicialmente tengo un valor de 1V, el display del voltímetro me mostraría 01 V, si yo aumento este valor hasta 1.7V, me mostraría 1V. Sólo puede cambiar hasta que el voltaje de entrada rebasara los 2V. En este caso el cambio no es continuo, cada cambio en el dígito del display, representa 1 voltio.
¿Cómo diferenciar un valor Analógico de uno Digital?
La diferencia más obvia entre un valor Analógico y otro Digital se puede determinar fácilmente de la siguiente manera:
- Valor Analógico - Representación continua de cantidades.
- Valor digital - Representación paso a paso de cantidades.
Los valores Digitales, no dejan espacio a dudas ni interpretaciones, ya que su cantidad puede estar dentro de un amplio rango de medidas, pero tiene un solo valor.
Ventajas de los sistemas Digitales.
Cada vez aumenta más el número de usos en el campo de la electrónica (y en muchos otros campos) para los sistemas digitales, en los cuáles reinaban los sistemas análogos. Muchas son las razones para este cambio, algunas de las más importantes son:
- En general, los sistemas digitales son fáciles de diseñar.
Esta propiedad se debe a que no es necesario aplicar voltajes exactos a los circuitos digitales, por el contrario, sólo es necesario que los voltajes permanezcan o alcancen los niveles de operación para cada estado lógico (ALTO o BAJO). - Capacidad de almacenar retener información.
Muchos de los circuitos digitales tienen un solo propósito, el de almacenar, retener, y enviar información a voluntad del usuario. - Funcionamiento programado.
Es muy fácil que un circuito digital siga una serie de órdenes llamadas PROGRAMAS, grabados dentro de los mismos. - Menor espacio para más circuitos.
Aunque la tecnología analógica ha avanzado mucho, sería imposible superar el tamaño de un circuito digital complicado, con su equivalente en circuitos analógicos.
Podemos lograr que un circuito digital haga lo cualquier cosa que necesitemos dentro de los parámetros del mundo digital, pero, ¿Cómo podemos hacer para que este circuito "comprenda" todos los valores de nuestro mundo, que por regla básica es completamente analógico?
Esta, es la única desventaja al utilizar sistemas digitales.
En su gran mayoría, las fuerzas físicas en el mundo real son analógicas, y los sistemas digitales las utilizan como entradas y salidas de información para efectuar las acciones que necesitemos con ellas, como medición y control.
Algunos ejemplos son:
- La temperatura.
- La presión.
- La velocidad.
- Niveles de un líquido.
Esta aproximación de valores un ejemplo claro de cómo podemos "traducir" los valores analógicos en valores digitales que nuestro circuito pueda interpretar y manipular sin problemas
Por consiguiente, para poder utilizar los sistemas digitales para trabajar con valores analógicos, se vuele prioridad seguir una serie de pasos, los cuáles serían:
- Convertir los valores analógicos a su equivalente digital.
- Utilizar esta información dependiendo de nuestras necesidades.
- Convertir de nuevo los valores procesados a su estado analógico.

Dentro del mundo digital, se utilizan varios sistemas de numeración, de estos, los de uso común son:
- El sistema DECIMAL.
- El sistema BINARIO.
- El sistema OCTAL.
- El sistema HEXADECIMAL.
El sistema DECIMAL, está formado por diez símbolos (numerales), 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Para poder expresar una cantidad es necesario utilizar estos símbolos como dígitos de un número.
En el sistema decimal, cada número (además de su valor numeral) toma su valor dependiendo de la posición donde se encuentre colocado dentro del número.

Pongamos el ejemplo del número 1495, siguiendo la tabla arriba mencionada, sabemos que:
- El primer dígito (dígito más significativo - MSD en inglés) es 1 X1000 = 1 millar.
- El segundo dígito es 4 X100 = 4 centenas.
- El tercer dígito es 9 X10 = 9 decenas.
- El cuarto dígito (dígito menos significativo - LSD en inglés) es 5 X1 = 5 unidades.
2.- Sistema Binario
Debido a su naturaleza analógica, el sistema decimal no es útil si la intención es diseñar un circuito digital, ya que tenemos 10 diferentes números para trabajar, lo que causaría un enorme trabajo para poder realizar hasta las tareas más sencillas.
Basados en esta complicación, al diseñar los circuitos digitales se optó por un sistema mucho más eficaz para este tipo de trabajo, La manera más fácil de trabajar sería teniendo solamente dos niveles de voltaje, dos variables. Así se llegó a la solución de utilizar el sistema BINARIO (base 2), como base principal para los circuitos digitales, aunque no exclusiva.
En el sistema Binario, los numerales toman su valor de manera posicional (como el decimal), cada dígito binario utiliza su propio valor expresado a la potencia de 2.
En este sistema, por abreviación, el Dígito Binario se nombra como BIT, Quedando la tabla para un número de 4 bits como sigue:

Resumiendo, en un número de cuatro bits, el valor de cada bit dependiendo de su posición es calculado fácilmente con la siguiente tabla:

En un número de ocho bits quedaría como:

Conteo Binario
En la siguiente tabla usaremos un número de 4 bits para crear un conteo, al inicio de al cuenta, todos los bits están en cero.
Con cada conteo, el LSB cambia su valor de un número binario al otro, cada vez que este cambia de 1 a 0, el segundo bit cambia de estado también, cuando los dos primeros bits cambian de 1 a 0, el tercer bit cambia su estado, y cuando los tres primeros bits cambian de 1 a 0, cambia el MSB.
En la siguiente tabla s e muestra el conteo Binario de un número de cuatro Bits:

Observando con detalle la tabla anterior, se llega a la conclusión de que el conteo binario tiene una muy marcada característica:
- El primer Bit (LSB) (Bit con valor "1") cambia de 0 a 1 o de 1 a 0 con cada avance del conteo.
- El segundo Bit (Bit con valor "2") se mantiene dos conteos en 1 y dos en 0.
- El tercer Bit (Bit con valor "4") se mantiene por cuatro conteos en 1 y cuatro en 0.
- El cuarto Bit (MLB) (Bit con valor "8") se mantiene por ocho conteos en 1 y ocho en 0.
3.- Sistema Octal
El sistema de numeración octal es también muy utilizado en los sistemas digitales, la diferencia frente al sistema Binario es que sólo puede tener ocho posibles dígitos 0, 1, 2, 3, 4, 5,6 ,7. Por lo tanto, cada Bit de un número Octal sólo puede un valor del 0 al 7.

Conteo Octal
El mayor dígito del sistema Octal es el 7, por lo que cuando hacemos un conteo hacia arriba se incrementa un dígito por conteo, al llegar al número 7, se reinicia la cuenta de ese bit y al siguiente se le incrementa su conteo un dígito.
4.- Sistema Hexadecimal
El sistema de numeración hexadecimal (Hex), es parecido al sistema octal, pero con la diferencia que es base 16, por lo que puede tener hasta 16 símbolos (numerales), utilizando dígitos de la A a la F para representar los números del 10 al 15. Quedando: 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
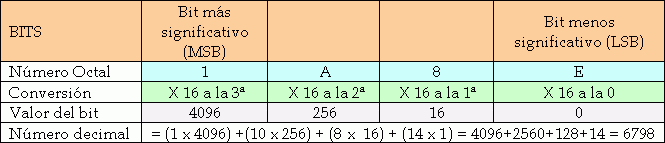
Conteo Hexadecimal
El mayor número del sistema Hexadecimal (Hex) es el 15, por lo que cuando hacemos un conteo hacia arriba se incrementa un dígito por conteo, al llegar a la F (15), se reinicia la cuenta de ese Bit y al siguiente de le incrementa su conteo un dígito:
Primer conteo = 28, 29, 2A, 2B, 2C, 2D, 2E, 2F, 30, 31, 32...
Segundo conteo = 5F8, 5F9, 5FA, 5FB, 5FC, 5FD, 5FE, 5FF, 600, 601, 602...
Segunda parte: Conversiones entre códigos.


