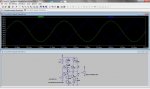
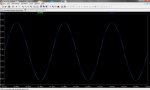
Hola chicos.
Hace unos días alguien preguntó sobre proyectos con operacionales, y yo le propuse un circuito cuyo uno de los bloques es una función parabólica, es decir, el voltaje de salida es el voltaje de entrada elevado al cuadrado.
El caso es que estuve pensando que debería de haber alguna forma sencilla de crear una parábola, aunque sea aproximada (es decir, que lo que nos interesa sea una forma parabólica, aunque el valor exacto cambie ligeramente con las condiciones de trabajo, temperatura, etc), ya que un bloque con dicha función puede ser muy útil para ciertos aspectos.
El caso es que el bloque implementado con operacionales utiliza la propiedad que tiene el diodo de emisor-base de un transistor (y en general cualquier diodo, pero nos interesa este) cuya corriente a su través es una función exponencial de su voltaje, o dicho a la inversa, el voltaje es una función logarítmica de la corriente que pasa a su través. En realidad la base de la exponencial y el logaritmo da igual, siempre que podamos aplicar una función y su inversa con la misma base, que podemos llamar p.
Lo dicho se puede resumir así:
[LATEX]\\V_{be}=log_p(I_b)\leftrightarrow I_b=p^{v_{be}}[/LATEX]
Ahora supongamos que tenemos una corriente de entrada (el voltaje de entrada se puede transformar en una corriente con una simple resistencia) a nuestro dispositivo. Para empezar quiero tener un voltaje que sea dependiente logarítmico de la corriente, eso lo podemos conseguir con un transistor realimentado negativamente desde el colector a la base, ya que,
[LATEX]\\V_{ce}= log_p(\frac{\beta+1}{\beta}*I_c)\approx log_p(I_c)[/LATEX]
ahora bien, quiero tener el doble de voltaje porque voy a utilizar la propiedad de los logaritmos de que si multiplico por 2 el logaritmo, es como elevar al cuadrado lo que hay dentro de el, lo primero que se viene a la cabeza es usar un amplificador x2 del Vce de nuestro transistor realimentado, pero si lo pensamos bien, dos transistores puestos en serie, nos van a hacer el mismo papel ya que va a pasar la misma corriente por ambos, y entonces la caida de ambos transistores será 2*log(Ic). Ahora para convertir a una corriente I de salida, si usamos un transistor tenemos el problema que la base va a chupar corriente antes de que ambos transistores de entrada comiencen a conducir. Además la parábola va a estar multiplicada por el factor beta de la corriente Ic con respecto a la corriente Ib del transistor de salida. Ambos problemas se arreglan bastante bien simplemente añadiendo un seguidor de emisor. La resistencia de emisor a tierra va a polarizar el diodo base-emisor para que con muy poca variación haya una caida de tensión de aproximadamente 0.6V, y el transistor va a funcionar de buffer de corriente, separando el convertidor logaritmico del convertidor exponencial, y además anulando el efecto de la ganancia del transistor de salida, de manera que I salida sea la I de entrada al cuadrado (con algún pequeño margen de error).
Así pues,
[LATEX]\\I_c=\beta *I_b=\beta*p^{V_{be}}[/LATEX]
[LATEX]\\I_{out}=\beta*p^{2*log_p(I_{in})-0.6}= \beta*\frac{I^2_{in}}{p^{0.6}} \rightarrow \beta\approx p^{0.6}\rightarrow I_{out}=I^2_{in}[/LATEX]
Colocando una resistencia en el colector del transistor de salida y en los de entrada, convierto todo esto en (Vout=Vcc-(Vin-1.2)^2 donde 1.2V es dos veces 0.6V, el voltaje para que comience a funcionar los dos transistores que convierten corriente a un voltaje logarítmico). Nuestra función va a funcionar desde 1.2V hasta Vcc, que por conveniencia establezco en 5V. Como la función logaritmica no acepta voltajes negativos, ni si quiera el voltaje 0, voy a añadir un bloque, antes de nuestro convertidor parabólico, que convierta nuestra señal en una señal cuyo 0 sea 1.2V y ya sea que vaya hacia arriba o hacia abajo de ese valor, la salida de dicho bloque siempre vaya hacia arriba. Lo que voy a hacer va a ser un rectificador de onda completa centrado en Vcc/2, seguido de un buffer que además me desplazará el voltaje hasta 1.2V aproximadamente.
El rectificador de onda completa de precisión lo voy a hacer con un simple transistor. No estoy bromeando, estoy usando la propiedad de inversión de fase que tiene un transistor en emisor comun cuando éste se satura. De manera que construyendo un amplificador de ganancia unidad, tendremos en la zona directa una inversión de fase de Vcc-Vin-0.6V, y en la zona donde el colector se aproxima a Vcc/2, a partir de ahí tenemos que la salida es Vin+0.6-Vcc/2, incluso cuando Vin supera el valor de Vcc. Luego usaré un seguidor de emisor, colocando en la base un diodo que haga que caiga 0.7V (ajustable jugando con la resistencia de emisor del seguidor) mas sumado la caida del seguidor de emisor, tenemos 1.3V, y como nuestra Vcc=5V y por lo tanto el mínimo del rectificador de onda completa es de Vcc/2=2.5V, tenemos que en la entrada de nuestra parabola tenemos una señal que va desde 3.7V hasta 1.2V, y vuelve a subir de nuevo hasta 3.7V, que es como queríamos.
Juntando ambos bloques, nos queda la siguente función:
[LATEX]V_{out}=5-(V_{in}-3.1)^2\\[/LATEX]
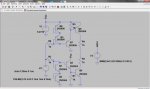
Implementando todo esto en LTspice, nos queda el siguiente esquema:

Aquí lo importante es que todos los transistores, o al menos los del bloque parabolico, sean todos con las betas muy similares, y como es algo muy importante, es algo en lo que ni me he fijado al implementar el circuito en protoboard, para variar...
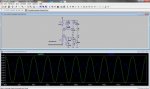
Vamos a simular el sistema metiendo en la entrada una rampa:
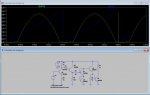
La simulación es consistente con los resultados. Si bien hice algo de trampa ya que hice la simulación después de haber probado el circuito en protoboard y ver que funcionaba.
Tener una parábola puede sernos bastante útil, por ejemplo para calcular valores eficaces en voltajes aunque sea aproximada, dentro de rangos del 5 al 10%, y la ventaja de hacerlo con transistores es que la respuesta es muchísimo más rápida que con operacionales, además de mucho más económica, aunque no sea tan precisa.
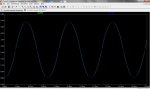
Por ejemplo, nos da igual si la amplitud de la parábola no es exacta, cuando lo que queremos es usar esa bonita propiedad de las parábolas que permite duplicar una senoidal sin importar su frecuencia:
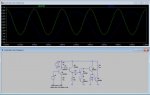
Como he dicho, el circuito lo había implementado antes en protoboard, tabulando los voltajes de entrada y salida. Esto que muestro a continuación son valores reales, no simulados:
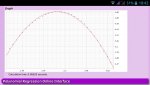
Aunque los valores se desvían un poco, hay que tener en cuenta el error en las medidas con el tester, ya que estamos hablando de apenas milivoltios de diferencia con la parábola calculada mediante regresión cuadrática, que por cierto, arroja una ecuación aproximada de Vo=5-(Vi-3.04)^2, bastante próximo a lo que habíamos calculado.
Luego vereis la implementación real.
Ahora vamos un paso más. Como he dicho, esta función se puede usar para muchas cosas útiles, por eso vamos a usar esta función para algo que no sirva para mucho, o al menos en apariencia, pero oye!! si funciona va a quedar bonito.
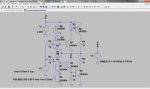
Vamos a poner un offset a nuestra parábola, lo voy a hacer con otro transistor conectado paralelamente al colector del transistor de salida, de forma que al polarizarlo me va a permitir ajustar una corriente en la resistencia que sumada a la del parabolizador, va a permitirme desplazar el punto del máximo de la parábola, y esto lo hago polarizando con un par de resistencias (o un potenciómetro) que polarizan la base de dicho transistor. Además la salida voy a ajustar su atenuación mediante un potenciómetro configurado como resistencia variable. Muy y bien, ¿y para qué todo esto? para meter la salida otra vez en la entrada y ver que ocurre. En principio tenemos un sistema dinámico no lineal. La ecuación es sencilla:
[LATEX]\\V_{n+\Delta n}=A*(5-((V_n-3.1)^2+B))[/LATEX]
Donde A representa la atenuación, y B el offset de la parábola. Replanteándonos la referencia de voltaje, podemos asumir 3.1V como nuestra nueva masa, de esa manera podemos tener voltajes positivos y negativos a su alrederdor, y así poder simplificar nuestra expresión- Además podemos simplicar el offset con una sencilla manipulación de variable:
[LATEX]\\V_{n+\Delta n}=A*(1.9-V_n^2+B)\rightarrow C=-B-1.9\rightarrow V_{n+\Delta n}=-A*(V_n^2+C)[/LATEX]
Esta ecuación, siendo una función de tiempo continuo es fácilmente resoluble, simplemente [latex]\Delta n[/latex] se aproxima a 0, y por lo tanto se puede pasar a la derecha la parte izquierda y tenemos una ecuación de segundo grado que presenta dos soluciones fijas. Este es el enfoque del simulador. Resolver interpolando cada paso de forma continua hasta que el resultado converge en una u otra solución:
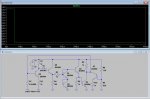
Pero, ¿Y si nuestro convertidor no es una función continua? ¿que pasa si el tiempo es discreto, es decir, que el tiempo [latex]\Delta n[/latex] no sea 0 sino que aun siendo pequeño representa el tiempo mínimo promedio entre que entra un electrón y el siguente al sistema? Esta ecuación es una vieja conocida, usada para generar fractales como Julia y Mandelbrot, y realimentada de manera discreta (para n=1,2,3...., es decir para delta de n=1), para valores de C negativos, la función presenta zonas oscilantes, otras zonas caóticas, etc.
¿Que pensais que pasará si implemento esto en un circuito real? ¿pasará como en el simulador, que dependiendo de las condiciones iniciales la salida irá rápidamente entre una y otra solución de la ecuación de segundo grado? ¿o tendremos caos? Podeis verlo vosotros mismos:
Espero que os haya gustado. Saludos.
Hace unos días alguien preguntó sobre proyectos con operacionales, y yo le propuse un circuito cuyo uno de los bloques es una función parabólica, es decir, el voltaje de salida es el voltaje de entrada elevado al cuadrado.
El caso es que estuve pensando que debería de haber alguna forma sencilla de crear una parábola, aunque sea aproximada (es decir, que lo que nos interesa sea una forma parabólica, aunque el valor exacto cambie ligeramente con las condiciones de trabajo, temperatura, etc), ya que un bloque con dicha función puede ser muy útil para ciertos aspectos.
El caso es que el bloque implementado con operacionales utiliza la propiedad que tiene el diodo de emisor-base de un transistor (y en general cualquier diodo, pero nos interesa este) cuya corriente a su través es una función exponencial de su voltaje, o dicho a la inversa, el voltaje es una función logarítmica de la corriente que pasa a su través. En realidad la base de la exponencial y el logaritmo da igual, siempre que podamos aplicar una función y su inversa con la misma base, que podemos llamar p.
Lo dicho se puede resumir así:
[LATEX]\\V_{be}=log_p(I_b)\leftrightarrow I_b=p^{v_{be}}[/LATEX]
Ahora supongamos que tenemos una corriente de entrada (el voltaje de entrada se puede transformar en una corriente con una simple resistencia) a nuestro dispositivo. Para empezar quiero tener un voltaje que sea dependiente logarítmico de la corriente, eso lo podemos conseguir con un transistor realimentado negativamente desde el colector a la base, ya que,
[LATEX]\\V_{ce}= log_p(\frac{\beta+1}{\beta}*I_c)\approx log_p(I_c)[/LATEX]
ahora bien, quiero tener el doble de voltaje porque voy a utilizar la propiedad de los logaritmos de que si multiplico por 2 el logaritmo, es como elevar al cuadrado lo que hay dentro de el, lo primero que se viene a la cabeza es usar un amplificador x2 del Vce de nuestro transistor realimentado, pero si lo pensamos bien, dos transistores puestos en serie, nos van a hacer el mismo papel ya que va a pasar la misma corriente por ambos, y entonces la caida de ambos transistores será 2*log(Ic). Ahora para convertir a una corriente I de salida, si usamos un transistor tenemos el problema que la base va a chupar corriente antes de que ambos transistores de entrada comiencen a conducir. Además la parábola va a estar multiplicada por el factor beta de la corriente Ic con respecto a la corriente Ib del transistor de salida. Ambos problemas se arreglan bastante bien simplemente añadiendo un seguidor de emisor. La resistencia de emisor a tierra va a polarizar el diodo base-emisor para que con muy poca variación haya una caida de tensión de aproximadamente 0.6V, y el transistor va a funcionar de buffer de corriente, separando el convertidor logaritmico del convertidor exponencial, y además anulando el efecto de la ganancia del transistor de salida, de manera que I salida sea la I de entrada al cuadrado (con algún pequeño margen de error).
Así pues,
[LATEX]\\I_c=\beta *I_b=\beta*p^{V_{be}}[/LATEX]
[LATEX]\\I_{out}=\beta*p^{2*log_p(I_{in})-0.6}= \beta*\frac{I^2_{in}}{p^{0.6}} \rightarrow \beta\approx p^{0.6}\rightarrow I_{out}=I^2_{in}[/LATEX]
Colocando una resistencia en el colector del transistor de salida y en los de entrada, convierto todo esto en (Vout=Vcc-(Vin-1.2)^2 donde 1.2V es dos veces 0.6V, el voltaje para que comience a funcionar los dos transistores que convierten corriente a un voltaje logarítmico). Nuestra función va a funcionar desde 1.2V hasta Vcc, que por conveniencia establezco en 5V. Como la función logaritmica no acepta voltajes negativos, ni si quiera el voltaje 0, voy a añadir un bloque, antes de nuestro convertidor parabólico, que convierta nuestra señal en una señal cuyo 0 sea 1.2V y ya sea que vaya hacia arriba o hacia abajo de ese valor, la salida de dicho bloque siempre vaya hacia arriba. Lo que voy a hacer va a ser un rectificador de onda completa centrado en Vcc/2, seguido de un buffer que además me desplazará el voltaje hasta 1.2V aproximadamente.
El rectificador de onda completa de precisión lo voy a hacer con un simple transistor. No estoy bromeando, estoy usando la propiedad de inversión de fase que tiene un transistor en emisor comun cuando éste se satura. De manera que construyendo un amplificador de ganancia unidad, tendremos en la zona directa una inversión de fase de Vcc-Vin-0.6V, y en la zona donde el colector se aproxima a Vcc/2, a partir de ahí tenemos que la salida es Vin+0.6-Vcc/2, incluso cuando Vin supera el valor de Vcc. Luego usaré un seguidor de emisor, colocando en la base un diodo que haga que caiga 0.7V (ajustable jugando con la resistencia de emisor del seguidor) mas sumado la caida del seguidor de emisor, tenemos 1.3V, y como nuestra Vcc=5V y por lo tanto el mínimo del rectificador de onda completa es de Vcc/2=2.5V, tenemos que en la entrada de nuestra parabola tenemos una señal que va desde 3.7V hasta 1.2V, y vuelve a subir de nuevo hasta 3.7V, que es como queríamos.
Juntando ambos bloques, nos queda la siguente función:
[LATEX]V_{out}=5-(V_{in}-3.1)^2\\[/LATEX]
Implementando todo esto en LTspice, nos queda el siguiente esquema:

Aquí lo importante es que todos los transistores, o al menos los del bloque parabolico, sean todos con las betas muy similares, y como es algo muy importante, es algo en lo que ni me he fijado al implementar el circuito en protoboard, para variar...
Vamos a simular el sistema metiendo en la entrada una rampa:

La simulación es consistente con los resultados. Si bien hice algo de trampa ya que hice la simulación después de haber probado el circuito en protoboard y ver que funcionaba.
Tener una parábola puede sernos bastante útil, por ejemplo para calcular valores eficaces en voltajes aunque sea aproximada, dentro de rangos del 5 al 10%, y la ventaja de hacerlo con transistores es que la respuesta es muchísimo más rápida que con operacionales, además de mucho más económica, aunque no sea tan precisa.
Por ejemplo, nos da igual si la amplitud de la parábola no es exacta, cuando lo que queremos es usar esa bonita propiedad de las parábolas que permite duplicar una senoidal sin importar su frecuencia:

Como he dicho, el circuito lo había implementado antes en protoboard, tabulando los voltajes de entrada y salida. Esto que muestro a continuación son valores reales, no simulados:

Aunque los valores se desvían un poco, hay que tener en cuenta el error en las medidas con el tester, ya que estamos hablando de apenas milivoltios de diferencia con la parábola calculada mediante regresión cuadrática, que por cierto, arroja una ecuación aproximada de Vo=5-(Vi-3.04)^2, bastante próximo a lo que habíamos calculado.
Luego vereis la implementación real.
Ahora vamos un paso más. Como he dicho, esta función se puede usar para muchas cosas útiles, por eso vamos a usar esta función para algo que no sirva para mucho, o al menos en apariencia, pero oye!! si funciona va a quedar bonito.
Vamos a poner un offset a nuestra parábola, lo voy a hacer con otro transistor conectado paralelamente al colector del transistor de salida, de forma que al polarizarlo me va a permitir ajustar una corriente en la resistencia que sumada a la del parabolizador, va a permitirme desplazar el punto del máximo de la parábola, y esto lo hago polarizando con un par de resistencias (o un potenciómetro) que polarizan la base de dicho transistor. Además la salida voy a ajustar su atenuación mediante un potenciómetro configurado como resistencia variable. Muy y bien, ¿y para qué todo esto? para meter la salida otra vez en la entrada y ver que ocurre. En principio tenemos un sistema dinámico no lineal. La ecuación es sencilla:
[LATEX]\\V_{n+\Delta n}=A*(5-((V_n-3.1)^2+B))[/LATEX]
Donde A representa la atenuación, y B el offset de la parábola. Replanteándonos la referencia de voltaje, podemos asumir 3.1V como nuestra nueva masa, de esa manera podemos tener voltajes positivos y negativos a su alrederdor, y así poder simplificar nuestra expresión- Además podemos simplicar el offset con una sencilla manipulación de variable:
[LATEX]\\V_{n+\Delta n}=A*(1.9-V_n^2+B)\rightarrow C=-B-1.9\rightarrow V_{n+\Delta n}=-A*(V_n^2+C)[/LATEX]
Esta ecuación, siendo una función de tiempo continuo es fácilmente resoluble, simplemente [latex]\Delta n[/latex] se aproxima a 0, y por lo tanto se puede pasar a la derecha la parte izquierda y tenemos una ecuación de segundo grado que presenta dos soluciones fijas. Este es el enfoque del simulador. Resolver interpolando cada paso de forma continua hasta que el resultado converge en una u otra solución:

Pero, ¿Y si nuestro convertidor no es una función continua? ¿que pasa si el tiempo es discreto, es decir, que el tiempo [latex]\Delta n[/latex] no sea 0 sino que aun siendo pequeño representa el tiempo mínimo promedio entre que entra un electrón y el siguente al sistema? Esta ecuación es una vieja conocida, usada para generar fractales como Julia y Mandelbrot, y realimentada de manera discreta (para n=1,2,3...., es decir para delta de n=1), para valores de C negativos, la función presenta zonas oscilantes, otras zonas caóticas, etc.
¿Que pensais que pasará si implemento esto en un circuito real? ¿pasará como en el simulador, que dependiendo de las condiciones iniciales la salida irá rápidamente entre una y otra solución de la ecuación de segundo grado? ¿o tendremos caos? Podeis verlo vosotros mismos:
Espero que os haya gustado. Saludos.
Última edición: