Dr. Zoidberg
Well-known-Papá Pitufo
Hace tiempo que venimos discutiendo acerca de la Transformación de Linkwitz (LT) para extender la respuesta en baja frecuencia de woofers y subwoofers, a pesar que eso es solo una de las aplicaciones posibles.
Si bien yo he usado la LT para conformar la respuesta de woofers y también de tweeters, no teníamos en el foro un PCB que nos permitiera usarlo sin restricciones, por que el modelo que yo he usado está fuertemente basado en el diseño del Proyecto 71 de ESP y por ende prefiero no publicarlo.
Ahora he desarrollado un PCB nuevo, que si bien conserva parte de lo que diseñó ESP, he cambiado las resistencias en serie por solo pares en paralelo, que es lo que recomienda D. Self por que es mas fácil hacer el PCB y mas económico.
En principio, parece más facil poner resistencias en serie para llegar al valor deseado, y de hecho es como uno lo piensa, por que es mas simple calcular [LATEX]Ra+Rb[/LATEX] que [LATEX]\dfrac{Ra*Rb}{(Ra+Rb)}[/LATEX]. Resulta que D. Self habla de que en su sitio web hay un soft que calcula y optimiza el paralelo, pero como nunca logré encontrarlo tuve que escribir el mío y se los comparto. No les doy el código fuente - por ahora - por que es una versión pre-beta , pero no tiene errores hasta donde lo probé. Es una app de consola y recibe los parámetros de la línea de comando y muestra los resultados a los que llega (bien a lo macho de UNIX, pero corre en una ventana de DOS
, pero no tiene errores hasta donde lo probé. Es una app de consola y recibe los parámetros de la línea de comando y muestra los resultados a los que llega (bien a lo macho de UNIX, pero corre en una ventana de DOS  ). Aún no optimiza el paralelo (las resistencias deben ser lo más cercanas entre sí en valor para aumentar la precisión y reducir la tolerancia estadística... lean a D. Self en "The design of active crossovers") por que el tema dá para largo).
). Aún no optimiza el paralelo (las resistencias deben ser lo más cercanas entre sí en valor para aumentar la precisión y reducir la tolerancia estadística... lean a D. Self en "The design of active crossovers") por que el tema dá para largo).
El programa se llama ResistenciaParalelo.exe y está en el archivo ResistenciaParalelo.zip. Se invoca manualmente desde una consola DOS (Inicio->Ejecutar->cmd Enter), pero supongo que todos saben manejar DOS y Windows, así que vamos al grano:
El programa acepta 3 parámetros en la línea de comandos:
Primero: Serie de resistencias a usar --> E12 o E24 (e12 o e24... da lo mismo)
Segundo: Tolerancia máxima permitida [%] --> 0.5 ó 0.25 va bien, pero pueden probar otras.
Tercero: Valor de resistencia a encontrar usando otras dos en paralelo. OJO con este parámetro, que debe ser >= 1.0 y <10.0, por que el soft aún no normaliza. Si ustedes necesitan 1470Ω van a tener que poner 1.47 y luego multiplicar el resultado por 1000...se entendió????
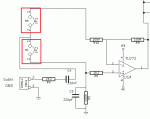
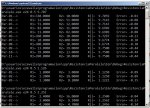
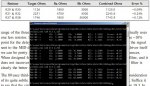
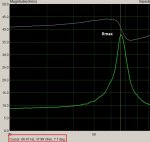
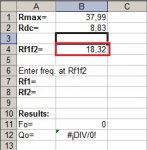
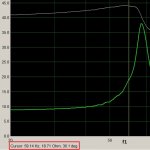
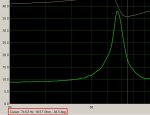
El soft tiene limitada a 100 la cantidad de iteraciones en búsqueda de la solución, así que si el soft les tira cualquier verdura, es que no hay solución con la serie de valores que usaron y deben probar con la otra (si usaron E12 prueben con E24 y viceversa). Acá hay una imagen de lo que sucede:
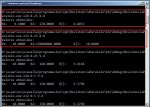
Los dos primeros ejemplos de los recuadros rojos buscan lograr una resistencia de 8.8, primero con la serie E24 y luego con E12. Con la E24 se obtiene un par de 9.1 en paralelo con 270, lo que resulta en 8.8033, mientras que el segundo logra 10 en paralelo con 270 millones y resulta en 10, lo que claramente no es solución con la combinación de serie y tolerancia usada, ergo, hay que usar dos resistencias de la serie E24 para conseguir el valor buscado o bien, aumentar la tolerancia del resultado. Luego hay otros ejemplos para buscar el mismo valor de resistencia en diferentes series y tolerancias. Mejor jueguen con el soft por que no dá para más la explicación.
Les recuerdo que es una versión pre-beta y está compilada en modo Debug, así que los que se quieran quejar, que hagan uno y lo compartan.
Ahora deberíamos conversar un poco acerca de algunas cosas del diseño heredado de ESP y del diseño de las ecuaciones de Linkwitz, pero les advierto: Esta ecualización es una herramienta MUY PODEROSA cuando el que la usa sabe lo que hace, pero usada al voleo pueden comerse un parlante o un amplificador antes de que se den cuenta, así que estudien y tenga cuidado.
Luego voy a agregar algunas planillas excel y procedimientos que son útiles para estimar el modelo a corregir con esta ecualización, pero por ahora ya tienen el PCB y el soft para calcular las resistencias que surjan de aplicar las ecuaciones de Linkwitz.
IMPORTANTE:
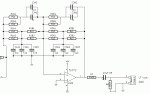
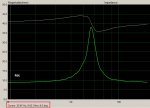
No hay muchas diferencias entre este PCB y el que yo he usado en mis diseños, así que debería funcionar sin problemas. El PCB está ruteado en base al net-list del esquemático, y todo lo que está antes y después de la doble-T puenteada está 100% probado y operativo. Tengo que armar un PCB nuevo y ensayarlo con el ARTA para validar la curva de respuesta, pero estoy 100% seguro que funciona a la perfección. Si alguien tiene dudas, puede armar un PCB, ponerle los componentes necesarios y verificar la curva de respuesta con el ARTA, por que yo me voy a demorar un poco en hacerlo.
DISCLAIMER:
Como de costumbre, pueden usar este diseño para lo que quieran cobrandolo o regalándolo, pero NO LE PUEDEN QUITAR MI NOMBRE DEL PCB, está claro???? El que lo haga será mas ladrón que los directivos de la AFA, de la FIFA y los funcionarios del anterior gobierno. Tampoco tengo responsabilidad alguna por lo que les que suceda usando este diseño, por que se supone que quien lo usa sabe lo que está haciendo. Por ello, si le queman la peluca a la vecina o le prenden fuego a su casa, la culpa solo es de ustedes, está claro????
Si bien yo he usado la LT para conformar la respuesta de woofers y también de tweeters, no teníamos en el foro un PCB que nos permitiera usarlo sin restricciones, por que el modelo que yo he usado está fuertemente basado en el diseño del Proyecto 71 de ESP y por ende prefiero no publicarlo.
Ahora he desarrollado un PCB nuevo, que si bien conserva parte de lo que diseñó ESP, he cambiado las resistencias en serie por solo pares en paralelo, que es lo que recomienda D. Self por que es mas fácil hacer el PCB y mas económico.
En principio, parece más facil poner resistencias en serie para llegar al valor deseado, y de hecho es como uno lo piensa, por que es mas simple calcular [LATEX]Ra+Rb[/LATEX] que [LATEX]\dfrac{Ra*Rb}{(Ra+Rb)}[/LATEX]. Resulta que D. Self habla de que en su sitio web hay un soft que calcula y optimiza el paralelo, pero como nunca logré encontrarlo tuve que escribir el mío y se los comparto. No les doy el código fuente - por ahora - por que es una versión pre-beta
El programa se llama ResistenciaParalelo.exe y está en el archivo ResistenciaParalelo.zip. Se invoca manualmente desde una consola DOS (Inicio->Ejecutar->cmd Enter), pero supongo que todos saben manejar DOS y Windows, así que vamos al grano:
El programa acepta 3 parámetros en la línea de comandos:
Primero: Serie de resistencias a usar --> E12 o E24 (e12 o e24... da lo mismo)
Segundo: Tolerancia máxima permitida [%] --> 0.5 ó 0.25 va bien, pero pueden probar otras.
Tercero: Valor de resistencia a encontrar usando otras dos en paralelo. OJO con este parámetro, que debe ser >= 1.0 y <10.0, por que el soft aún no normaliza. Si ustedes necesitan 1470Ω van a tener que poner 1.47 y luego multiplicar el resultado por 1000...se entendió????
El soft tiene limitada a 100 la cantidad de iteraciones en búsqueda de la solución, así que si el soft les tira cualquier verdura, es que no hay solución con la serie de valores que usaron y deben probar con la otra (si usaron E12 prueben con E24 y viceversa). Acá hay una imagen de lo que sucede:

Los dos primeros ejemplos de los recuadros rojos buscan lograr una resistencia de 8.8, primero con la serie E24 y luego con E12. Con la E24 se obtiene un par de 9.1 en paralelo con 270, lo que resulta en 8.8033, mientras que el segundo logra 10 en paralelo con 270 millones y resulta en 10, lo que claramente no es solución con la combinación de serie y tolerancia usada, ergo, hay que usar dos resistencias de la serie E24 para conseguir el valor buscado o bien, aumentar la tolerancia del resultado. Luego hay otros ejemplos para buscar el mismo valor de resistencia en diferentes series y tolerancias. Mejor jueguen con el soft por que no dá para más la explicación.
Les recuerdo que es una versión pre-beta y está compilada en modo Debug, así que los que se quieran quejar, que hagan uno y lo compartan.
Ahora deberíamos conversar un poco acerca de algunas cosas del diseño heredado de ESP y del diseño de las ecuaciones de Linkwitz, pero les advierto: Esta ecualización es una herramienta MUY PODEROSA cuando el que la usa sabe lo que hace, pero usada al voleo pueden comerse un parlante o un amplificador antes de que se den cuenta, así que estudien y tenga cuidado.
Luego voy a agregar algunas planillas excel y procedimientos que son útiles para estimar el modelo a corregir con esta ecualización, pero por ahora ya tienen el PCB y el soft para calcular las resistencias que surjan de aplicar las ecuaciones de Linkwitz.
IMPORTANTE:
No hay muchas diferencias entre este PCB y el que yo he usado en mis diseños, así que debería funcionar sin problemas. El PCB está ruteado en base al net-list del esquemático, y todo lo que está antes y después de la doble-T puenteada está 100% probado y operativo. Tengo que armar un PCB nuevo y ensayarlo con el ARTA para validar la curva de respuesta, pero estoy 100% seguro que funciona a la perfección. Si alguien tiene dudas, puede armar un PCB, ponerle los componentes necesarios y verificar la curva de respuesta con el ARTA, por que yo me voy a demorar un poco en hacerlo.
DISCLAIMER:
Como de costumbre, pueden usar este diseño para lo que quieran cobrandolo o regalándolo, pero NO LE PUEDEN QUITAR MI NOMBRE DEL PCB, está claro???? El que lo haga será mas ladrón que los directivos de la AFA, de la FIFA y los funcionarios del anterior gobierno. Tampoco tengo responsabilidad alguna por lo que les que suceda usando este diseño, por que se supone que quien lo usa sabe lo que está haciendo. Por ello, si le queman la peluca a la vecina o le prenden fuego a su casa, la culpa solo es de ustedes, está claro????
Adjuntos
Última edición: