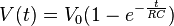Buenas,
Es un tema peliagudo No he visto nada en google que me aclare..
No he visto nada en google que me aclare..
Estamos haciendo en clase generadores de onda triangular y cuando me dijeron que el condensador se carga linealmente con corriente constante, me quede atonito

Entiendo que la carga sea lineal si la corriente es lineal (lógico).
Me gustaria saber, a ser posible con el minimo de matematicas, porque el condensador se craga exponencialmente..¿Temas de material de fabricacion?¿Cuestiones fisicas?¿Que es lo que hace variar una corriente constante de carga para que carge linealmente?
Espero que se entienda mi duda.
Saludos.
Es un tema peliagudo
Estamos haciendo en clase generadores de onda triangular y cuando me dijeron que el condensador se carga linealmente con corriente constante, me quede atonito
Entiendo que la carga sea lineal si la corriente es lineal (lógico).
Me gustaria saber, a ser posible con el minimo de matematicas, porque el condensador se craga exponencialmente..¿Temas de material de fabricacion?¿Cuestiones fisicas?¿Que es lo que hace variar una corriente constante de carga para que carge linealmente?
Espero que se entienda mi duda.
Saludos.