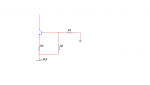
Ese es el típico circuito que tiene fuente doble, y arriba de esa fuente de corriente hay un diferencial conectado a la tensión positiva.
Tus ecuaciones ahí son:
[LATEX]I_{cq} \approx I_{eq}[/LATEX]
[LATEX]-V_{ee}=V_{R1}+V_{be}+I_{cq}.R_{e}[/LATEX]
[LATEX]-V_{ee}=V_{R1}+V_{R2}[/LATEX]
[LATEX]I_{R1}=I_{bq}+I_{R2}[/LATEX]
[LATEX]I_{bq}=\frac{I_{cq}}{H_{fe}}[/LATEX]
Tu idea es imponer Icq con esa fuente de corriente, entonces para facilitar el cálculo, suponés que Ir1>>Ibq, para eso usas valores "piolas" de R1 y R2

:
[LATEX]I_{R1} \approx I_{R2}[/LATEX]
Podés aproximar a un divisor resisitivo porque las corriente son casi iguales, el transistor casi no lo carga.
[LATEX]V_{R2} \approx \frac{R2}{R2+R1}.\left(-V_{ee}\right)[/LATEX]
De ahí sale Re:
[LATEX]V_{R2}=V_{be}+I_{cq}.R_{e} \rightarrow R_{e}=\frac{V_{R2}-V_{be}}{I_{cq}}[/LATEX]
Ejemplo, supongamos que Icq=2mA, Hfe=100, Vbe=0,7v y Vee=-12v:
[LATEX]I_{bq}=\frac{I_{cq}}{H_{fe}}=20 uA[/LATEX]
La corriente que deberá circular por R1 y R2 debe ser mucho más grande que Ibq para despreciarla y usar la fórmula del divisor resistivo, entonces:
[LATEX]I_{r1} \approx I_{r1} > 10. I_{bq}[/LATEX]
Con 200uA alcanza para hacer esa aproximación:
[LATEX]R_{1}+R_{2}=\frac{-Vee}{I_{r1}}=60 k\Omega[/LATEX]
Entre R1 y R2 no deberías sobrepasar los 60kOhms para mantenerse esa igualdad. Imponemos el valor de R1 y R2:
[LATEX]R1=R2=27 k\Omega \rightarrow V_{R2} \approx \frac{R2}{R2+R1}.\left(-V_{ee}\right)= 6v[/LATEX]
Ya estás en condiciones de obtener Re:
[LATEX]R_{e}=\frac{V_{R2}-V_{be}}{I_{cq}}=\frac{6v-0,7v}{2mA} \approx 2,7k\Omega[/LATEX]
Creo no equivocarme en nada, pero verificalo.
Te dejo la simulación, da bastante cerca y podés ver como funciona la aproximación que hice con las corrientes de R1 y R2:
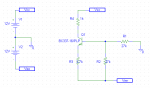
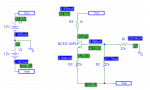
Fijate que la corriente de base para el Bc337 solo necesita 9uA, entonces esa será la diferencia entre IR1 e IR2, bastante despreciable frente a los 200uA que supuse.