¿ Realmente merecen la pena los cables para altavoces de precios elevados ?
Este artículo ofrece información para tener un buen criterio a la hora de decidir y también contribuye a entender.
Extractado de la revista Elektor
Un purista podría decir que si algo vale la pena hacerse, es mejor hacerlo bien
A finales de los años 70º aparece un nuevo producto para los “Puristas” del audio: “Los cables de elevadas prestaciones” (La marca se omitió para protección del autor), los cuales son cables de altavoz de elevado precio y de grueso calibre.
El viejo purismo apareció después, recordando el efecto de la resistencia de los cables en el factor de atenuación y el efecto de la capacidad del cable en la respuesta a altas frecuencias, añadiendo también la mención del efecto de superficie, el cual tiene que ver con el hecho de que a elevadas frecuencias, las corrientes alternas tienden a viajar principalmente a través de la superficie exterior del conductor.
Como el efecto de superficie tiende a reducir la corriente del centro del conductor, se reduce de forma efectiva el área de la sección del cable, provocando un aumento de su impedancia a elevadas frecuencias.
Realmente, cuando una frecuencia es lo suficientemente elevada, cualquier tubo o cañería puede tener la misma resistencia efectiva que un cable con el mismo diámetro. Este hecho se puede utilizar de forma simplificada para considerar el uso de guías de onda en lugar de cables para realizar el cableado a las frecuencias de las microondas.
Pero considerando la frecuencia, ¿Cuál es la magnitud del efecto?
Se supone que el efecto superficial comienza a ser importante por encima de unos 30 MHz. pero un añadido reciente para los cables de audio proclamaba que se podían obtener beneficios perceptibles mediante la reducción del efecto de superficie a 20 KHz.
Poco después, aparecieron artículos amparados en publicaciones profesionales de las marcas que mencionaban efectos de las guerras de las galaxias obtenidos mediante la utilización de los cables de grandes dimensiones, así como que se estaban realizando algunas investigaciones serias al respecto ¿?¿?¿?.
La meta era la de investigar si realmente los cables de grandes dimensiones hacían, de hecho, lo siguiente:
• Reducir la cantidad de potencia perdida en el cable en una cantidad suficiente como para mejorar la eficacia, o
• Incrementar el factor de amortiguamiento de sistema altavoz /amplificador lo suficiente como para lograr una mejora audible, o
• Proporcionar una mejora significante en la respuesta en frecuencia del sistema.
No se han mencionado otros beneficios a obtener con el uso de este tipo de cables, por ello, no es necesario buscar efectos no descubiertos o indetectables en la actualidad.
Este problema ha sido analizado tanto analíticamente como expo-mentalmente.
Este circuito es aproximadamente equivalente a un amplificador, un altavoz y a una cierta longitud de cable.
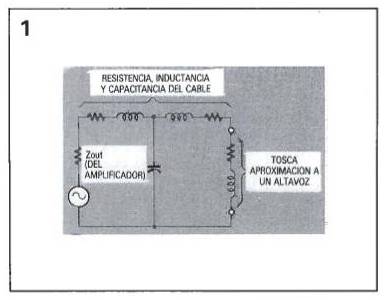
En la figura se puede ver el circuito equivalente de un altavoz real alimentado por un amplificador real a través de cables reales.
Cualquiera de los efectos introducidos por estos cable se deben mostrar en función de la resistencia, capacidad o inductancia de los mismos.
Las cuestiones relacionadas con la eficacia y el factor de amortiguamiento dependen casi exclusivamente de la resistencia del cable, mientras que las relaciones con la respuesta en frecuencia dependen principalmente de la capacidad.
La inductancia de los cables es tan pequeña comparada con la naturaleza semi-inductiva de la impedancia de los altavoces que se puede ignorar por completo, como se podrá ver más adelante.
La resistencia de los cables está formada por tres componentes básicos:
La resistencia de contacto.
La resistencia óhmica
Y cualquier contribución del efecto superficial.
La resistencia óhmica se puede obtener de forma sencilla en las tablas de la mayoría de los libros de referencia para electrónica.
Durante años, la selección de la sección de los cables se ha realizado en función del criterio del 10 por 100 de pérdidas.
En otras palabras, para una determinada longitud del cable, la resistencia del mismos no debe proporcionar unas pérdidas superiores al 10 por 100 (0.46 dB) en el altavoz.
Para longitudes de cable muy cortas, la sección de los mismos es sorprendentemente pequeña.
Unos quince años más tarde cuando el autor de nuestro artículo se convirtió en un asesor de audio solía especificar un cable de calibre 18 para amplificador de hasta 100 vatios que alimentaban a impedancias de 8 ohmios o más con longitudes de 8 metros o menos.
Por cada reducción a la mitad de la impedancia, o aumento de la potencia o la distancia al doble, el calibre 16 para alimentar 100 vatios sobre una impedancia de 8 ohmios a 16 metros o para alimentar una carga de 4 ohmios a 8 metros, etc.
Esta regla de amortiguamiento incorpora un margen de seguridad de forma que las pérdidas sean siempre inferiores al 10 por 100.
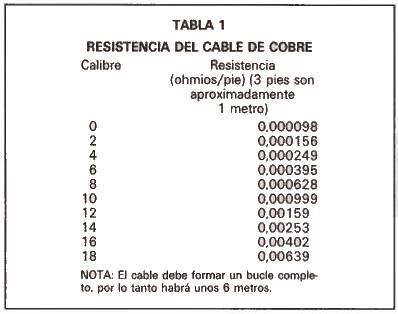
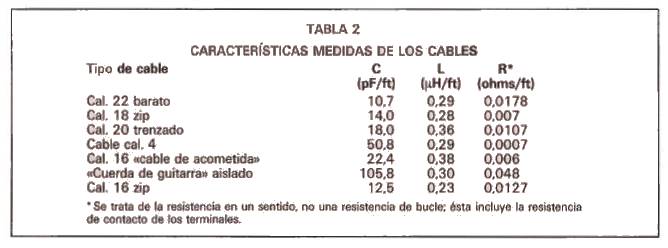
La tabla 1 muestra la resistencia de un conjunto representativo de cables de cobre, listada en función de la sección.
El código eléctrico nacional de EE.UU. especifica los calibres de los cables basados en consideraciones de seguridad:
Si un cable transporta una corriente muy elevada durante un tiempo muy grande se puede calentar de forma peligrosa y comenzar a arder.
Volviendo atrás sobre la regla anterior, un altavoz con una impedancia media de 8 ohmios alimentado por un amplificador de 100 vatios consumirá unos 3.5 amperios al máximo de potencia.
Sin embargo, incluso al tope máximo de potencia, es improbable que la potencia media sea superior a un tercio del máximo del amplificador, por este motivo la regla proporciona un margen de seguridad muy grande desde el punto de vista de la prevención de incendios.
El factor de amortiguamiento se puede definir como la relación entre la impedancia del altavoz y el total de la impedancia en serie colocada con respecto al altavoz.
Como el sencillo cálculo de pérdidas que se muestra en la figura 2 depende de la resistencia combinada del cable y el altavoz, la pérdida de potencia resistiva se puede relacionar con el factor de amortiguamiento.
De esta forma, se puede encontrar una relación entre el factor de amortiguamiento y las pérdidas a bajas frecuencias.
En la Audio Cyclopedia Howard Tremaine estableció que no hay ningún valor que permita obtener un factor de amortiguamiento mayor que 20.
Esto está basado en el hecho de que la resistencia de la bobina de un altavoz para sonidos vocales, aparece en el circuito y su valor es normalmente de 6 a 7.5 ohmios para un altavoz de 8 ohmios, lo que coloca un límite práctico a la hora de obtener mejoras reduciendo otras resistencias en el circuito.
El factor de amortiguamiento efectivo es igual a:
Factor Amortiguamiento = Z altavoz / (R bobina + R amplificador + R cable)
Para un determinado amplificador un factor de amortiguamiento de 20 puede representar una resistencia total de 8 ohms dividida por 20 o una resistencia de 0.4 ohmios en serie con el amplificador.
Esto podría dar un factor de amortiguamiento efectivo de:
8 Ohmios / (6 Ohmios * 0.4 ohmios) = 1.25
Suponiendo que la resistencia de la bobina es de 6 ohmios.
Con la mayoría de los amplificador que tienen impedancias de salida de 0,1 ohmios o inferiores, esto podría significar que la resistencia del cable podría ser de 0,3 ohmios.
Las pérdidas en decibelios correspondientes a un altavoz de 8 ohmios alimentado mediante un cable de 0,3 ohmios son:
= 20 log ( 8 Ohmios / 8 Ohmios + 0,3 Ohmios) = - 0,32db
Esto quiere decir que para obtener un factor de amortiguamiento óptimo, las pérdidas resistivas de los cables deben ser inferiores a 0,32 dB.
Este es un método tradicional usado normalmente para determinar el calibre de un cable en función de las pérdidas.
Sólo con el propósito de efectuar una comparación, consideremos un cable con unas pérdidas de 1 dB lo que podría resultar de una resistencia de cables de 0,9 ohmios y podría producir un factor de amortiguamiento de 1.14 (Que no es muy inferior a 1.25).
Como se mencionó anteriormente, el efecto superficial incrementa la impedancia efectiva del cable, lo que se puede explicar más fácilmente a la vista de la figura 3.
La profundidad de la corteza de un conductor es la distancia media sobre el conductor, desde la superficie exterior, hasta el punto cuya densidad de corriente es 1/e la densidad de corriente en la superficie. (La letra “e” es la base de los logaritmos naturales y es aproximadamente 2.72.)
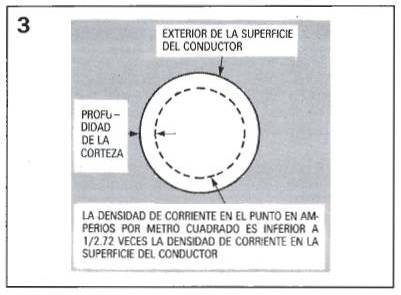
La profundidad de la corteza superficial es la distancia hacia el interior del conductor hasta alcanzar el punto cuya densidad de corriente es aproximadamente 1/3 de la existente en la superficie.
Para determinar a menos que se aísle cada trenza una de las otras, como ocurre en el cable de Litz.
De cualquier forma, se puede suponer que se trata de cable sólido como el caso peor para realizar los análisis, sabiendo que se está utilizando cable trenzado que tiene un menor efecto superficial.
La resistencia, capacidad e inductancia real de un cable se encuentra distribuida por igual a lo largo de su longitud.
Los ingenieros de teléfonos lo descubrieron hace mucho tiempo, así con el propósito de análisis, la resistencia, capacitáncia e inductancia de un cable se pueden agrupar en una componente simple si se cumplen una serie de condiciones.
Las condiciones dependen de la constante de atenuación y de la longitud del cable.
La constante de atenuación viene dada por la fórmula:
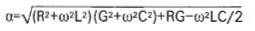
En la que R, L, C y G son la resistencia de cable, la capacitancia, la inductancia y las pérdidas por conductancia por unidad de longitud, es la frecuencia angular, o también (2 Pi * f) .
No es el propósito que quien lea esto se quede toda la noche analizando ecuaciones como ésta, y además las tablas de las constantes de atenuación en función de la frecuencia no se encuentran generalmente disponibles para los tipos de cable que se utilizan en el campo del audio.
Sin embargo, las tablas disponibles para los cables de calibre 19 para telefonía con aislamiento indican que se puede analizar una sección de cable de 3 kilómetros utilizando el método de las constantes agrupadas del cable a 1 KHz. con una atenuación total por debajo de 1 dB y con una precisión en fase dentro de los 5 grados aunque esto no puede quedar inmediatamente claro para el lector casual, la constante de atenuación es proporcional a la raíz cuadrada de frecuencia, de forma que significa que se puede obtener la misma precisión a 20 KHz si se reduce la longitud del cable según la expresión:
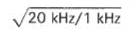
Como normalmente no se van a extender mucho los cables, sino más bien se van a mantener distancias cortas, se puede aplicar con seguridad el método de las constantes agrupadas sin lugar a dudas.
Esto es lo que se puede ver en la figura 1.
En lugar de un altavoz se ha utilizado una resistencia de 7,9 Ohmios y una inductancia de 6,3 uH para los cálculos.
En lugar de utilizar cables “de calibre exagerado”, se han empleado otros que se tenían a mano, incluyendo cables de larga longitud de calibre 4 trenzado.
Si estos cables no muestran detrimentos apreciables en la eficacia, factor de atenuación, o respuesta en frecuencia, entonces los cables de “exagerado calibre” se convierten en soluciones a problemas INEXISTENTES.
Una solución informaciónrmatizada del circuito de la figura 1 muestra los resultados que se pueden examinar en la figura 4.
Se ha asumido una longitud de 3 metros para cada cable, y se ha incluido el efecto de la capacidad e inductancia del cable, pero no se ha considerado el efecto de superficie.
Hay que señalar que en el peor de los casos las pérdidas se encontraban por debajo de 1 dB a 20 KHz.
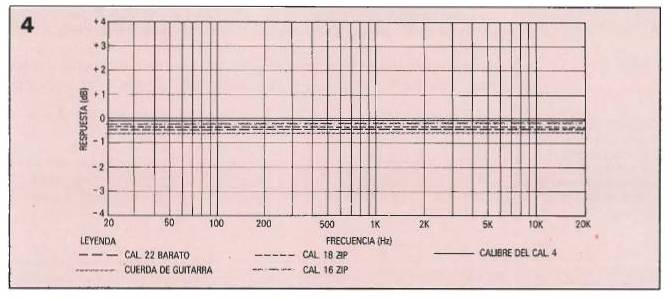
La solución obtenida con al ordenador, o predicción del modelo de la figura 1 arroja los resultados mostrados en esta figura.
La mayor pérdida en el peor de los casos arroja un valor de 1 dB a 20 KHz.
Este es el montaje utilizado para medir los efectos de los cables de altavoces sobre la señal de audio.
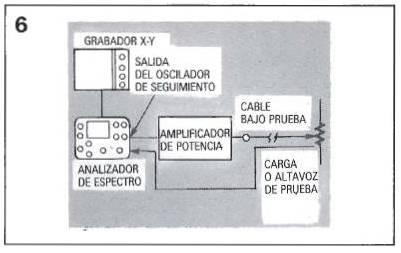
Las soluciones informaciónrmatizadas sin la verificación experimental no suelen ser muy fidedignas, por ello la respuesta real de los cables se midió con el montaje de la figura 5.
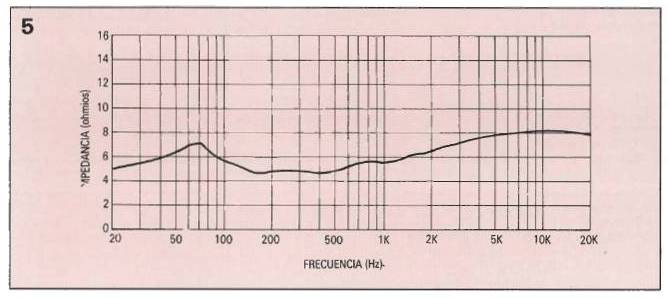
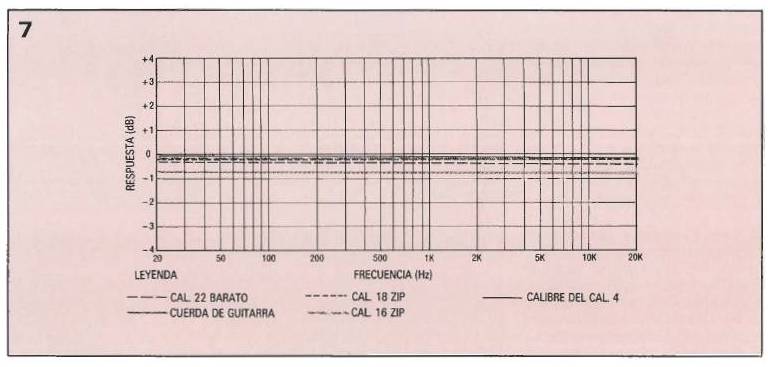
La impedancia característica del altavoz de prueba se muestra en la figura 6. Aunque el amplificador muestra una respuesta plana dentro de un margen +-0.2 dB entre 20 Hz y 20 KHz. la curva de calibración del amplificador sin embargo se obtuvo de los resultados de tal prueba se muestran en la figura 7.
Los resultados iniciales parecen indicar que se puede utilizar virtualmente casi todo para conectar un altavoz a un amplificador y si la distancia es suficientemente corta, no resulta un detrimento serio en la eficacia.
El factor de atenuación se degrada ligeramente cuando los cables tienen un calibre inferior al número 18 como se puede ver con unas pérdidas que superan los 0.32 dB. ¿Pero qué es lo que ocurre cuando se utilizan cables de longitudes superiores?
De las mediciones previas, se pudo comprobar que el cable Romex de conexionado tiene una capacidad superior a la de cualquier cable corriente.
Con el factor mencionado anteriormente que controla el efecto superficial, está claro también que los cables pequeños no experimentan un efecto superficial apreciable. aunque los grandes sí pueden mostrarlo en forma considerable, pero incluso un porcentaje de variación importante en la pequeña resistencia de un cable de grandes dimensiones ocasiona unas consecuencias despreciables.
Sin embargo, si cualquier tipo de cable de audio puede provocar problemas de frecuencia, la elevada capacidad y el efecto superficial del cable “Romex” del calibre 12 debería ser el “mal ejemplo” ideal.
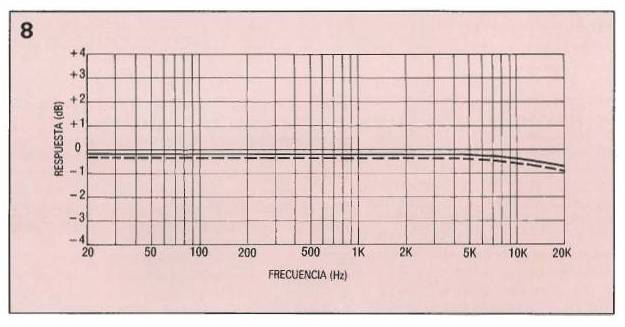
Se realizó otra prueba con un cable Romex de 14 metros de longitud, con una carga ficticia y con un altavoz de prueba.
En el gráfico de la figura 8 se puede ver una considerable caída de medio dB a 20 KHz comparada con la respuesta a 20 Hz.
La pérdida general de señal y la degradación del factor de amortiguación es inferior que aquella que se produce en cables de menor tamaño que se muestran en la figura 8 debido a la inferior resistencia del cable de calibre 12.
Como esto no era realmente significativo, se realizó una prueba con ordenador de 33 metros con el cable de calibre 10 de Romex con una respuesta de 50 KHz.
El resultado se muestra en la figura 9.
Aquí finalmente, los partidarios de los cables “De exagerado calibre” pueden clavar el diente en algo !
Cualquiera que pueda oír 50 KHz podrá encontrar una caída de 4.5 dB producida por la utilización de un cable de 33 metros de calibre 12 de Romex, por supuesto, teniendo un amplificador y un altavoz que lo pueda reproducir.
Como cabe esperar, el efecto superficial en los cables supone solamente medio decibelio aproximadamente y el amortiguamiento efectivo no se ve degradado, por ello quizá puedan mejorar su caída en esos puntos.
Aquí se puede observar tas pérdidas reales de los cables en comparación con las que se predicen en la figura 4,
Pérdida de señal sobre un cable de 13 metros Romex de calibre 12.
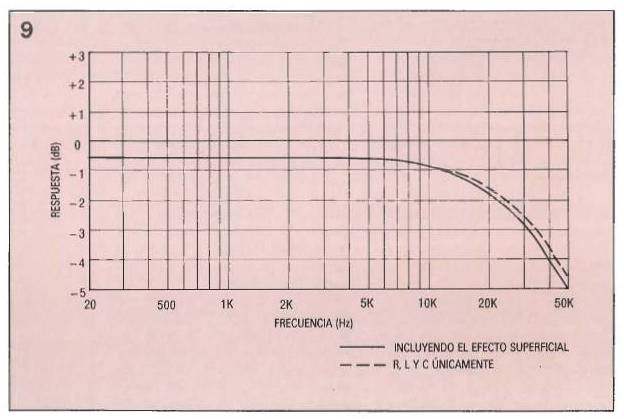
Pérdida de señal de 33 metros de cable Romex del calibre 12.
El resultado de todo esto es que en lugar de producirse una pequeña mejora en la búsqueda de la claridad de criterios, se indica claramente que estos cables ordinarios de altavoz, incluyendo aquellos que solamente los melómanos de reconocida sabiduría podrían despreciar, no suponen una degradación significativa en la respuesta en frecuencia.
Estos reivindican que la ley del “pulgar” recomienda un cable del calibre 18 para una potencia de 100 vatios sobre una longitud de 8 metros, para una carga de 8 ohmios, exceptuando el hecho de que se produce una pequeña degradación en el factor de amortiguamiento siendo éste de 1.21 con un cable de 8 metros.
Para obtener un factor de amortiguamiento óptimo se debe cambiar la regla por un cable de calibre 18 para una potencia de 100 vatios con una longitud de cable de 6 metros sobre 8 ohmios.
Sólo los cables de calibre 20 o 22 y los cables de cuerda de guitarra tienen problemas serios en lo que respecta al factor de amortiguamiento.
Última edición:












