A modo de experimentación y para iniciar un lindo debate, se me ocurrió jugar un rato con los instrumentos de LabVIEW en Multisim 14, aplicados a filtros pasabanda, para verificar qué sucede con la percepción de aquellos sonidos amortiguados que atraviesan un filtro pasabanda y cuyas frecuencias fundamentales caigan en las cercanías de las frecuencias de corte de los mismos filtros.
Resulta obvio que toda señal de riqueza espectral que atraviese un filtro va a perder personalidad en su timbre, pero el dilema se presenta cuando disponemos varios filtros pasabanda cubriendo todo el espectro de audio (supongamos 2, 3, 4 o más) y cuyas bandas no se superpongan. La intriga se da en los puntos de frecuencia donde un pasabanda empalma con el siguiente o el anterior, ya que existe un notorio cambio en la percepción de aquellos sonidos cuya frecuencia es coincidente o cercana a la frecuencia de esos empalmes.
Las preguntas del millón surgen: ¿Cuál vía adyacente a la frecuencia fundamental problemática reproducirá con más naturalidad el sonido? ¿Habrá limitaciones tanto en una y otra vía en reproducirlo con naturalidad? ¿Resulta más conveniente reducir o aumentar la cantidad de vías para minimizar el problema?.
Aquí las pruebas:
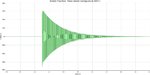
Se configuró un filtro pasabanda de segundo orden (12 dB por octava o 40 dB por década), con frecuencias de corte inferior en 40 Hz y superior en 4000 Hz.
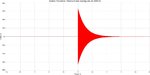
A la entrada de este filtro, se le inyectó tres tonos senoidales amortiguados de 40 Hz, 400 Hz y 4000 Hz, con ocurrencias cada 250 ms. Es decir, a tiempo 0, el tono de 40 Hz; a tiempo de 250 ms, el tono de 400 Hz y a tiempo de 500 ms, el tono de 4000 Hz. Como vemos, dos tonos coinciden con las frecuencias de corte del filtro, mientras que el tono de 400 Hz cae en el centro geométrico de la banda. Por la relación entre la frecuencia de los tonos y las frecuencias de corte del pasabanda, habrá tonos que sufrirán alteraciones perceptibles en el timbre y habrá un tono que sufrirá poco cambio perceptible (el de 400 Hz o centro de banda).
Lo que hice después fué grabar lo que sale del filtro pasabanda (archivo "con filtro pasabanda.rar") y compararlo con lo que entra al filtro (archivo "sin filtro pasabanda").
Luego, pueden escuchar y comparar por sí mismos y exponer en este thread sus conclusiones.
He hecho pruebas con filtros pasabandas de mayor orden e, incluso, el efecto es más notorio.
Resulta obvio que toda señal de riqueza espectral que atraviese un filtro va a perder personalidad en su timbre, pero el dilema se presenta cuando disponemos varios filtros pasabanda cubriendo todo el espectro de audio (supongamos 2, 3, 4 o más) y cuyas bandas no se superpongan. La intriga se da en los puntos de frecuencia donde un pasabanda empalma con el siguiente o el anterior, ya que existe un notorio cambio en la percepción de aquellos sonidos cuya frecuencia es coincidente o cercana a la frecuencia de esos empalmes.
Las preguntas del millón surgen: ¿Cuál vía adyacente a la frecuencia fundamental problemática reproducirá con más naturalidad el sonido? ¿Habrá limitaciones tanto en una y otra vía en reproducirlo con naturalidad? ¿Resulta más conveniente reducir o aumentar la cantidad de vías para minimizar el problema?.
Aquí las pruebas:
Se configuró un filtro pasabanda de segundo orden (12 dB por octava o 40 dB por década), con frecuencias de corte inferior en 40 Hz y superior en 4000 Hz.
A la entrada de este filtro, se le inyectó tres tonos senoidales amortiguados de 40 Hz, 400 Hz y 4000 Hz, con ocurrencias cada 250 ms. Es decir, a tiempo 0, el tono de 40 Hz; a tiempo de 250 ms, el tono de 400 Hz y a tiempo de 500 ms, el tono de 4000 Hz. Como vemos, dos tonos coinciden con las frecuencias de corte del filtro, mientras que el tono de 400 Hz cae en el centro geométrico de la banda. Por la relación entre la frecuencia de los tonos y las frecuencias de corte del pasabanda, habrá tonos que sufrirán alteraciones perceptibles en el timbre y habrá un tono que sufrirá poco cambio perceptible (el de 400 Hz o centro de banda).
Lo que hice después fué grabar lo que sale del filtro pasabanda (archivo "con filtro pasabanda.rar") y compararlo con lo que entra al filtro (archivo "sin filtro pasabanda").
Luego, pueden escuchar y comparar por sí mismos y exponer en este thread sus conclusiones.
He hecho pruebas con filtros pasabandas de mayor orden e, incluso, el efecto es más notorio.
Adjuntos
Última edición: