Curiosidades matemáticas

[asherar]

Puse esto aquí para separarlo de los acertijos de lógica y comprensión, ya que a algunos no les agrada demasiado el álgebra.

Les propongo ver algo práctico.

En el cálculo de impedancia de antenas, aparecen integrales de superficie singulares: el denominador R puede anularse. Para poder hacer la cuenta se debe factorear el cero del denominador mediante un cambio de variables (transformación de Duffy). En el caso que las nuevas coordenadas son x y w, y luego de todas las cuentas aburridas, la transformación del denominador queda:

R = w √ [ a1 + a2 x² + 2 a3 x ]

con los coeficientes constantes: a1 = L1², a2 = L2², a3 = L1 L2 cos [LATEX]a[/LATEX]. Las "L" son los largos de los lados del triángulo donde se va a integrar (ver figura).
Ver el archivo adjunto 81197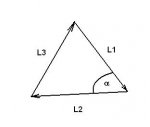
Los rangos de las variables son: 0 <= x <= 1, y 0 <= w <= 1

Si w = 1:
a) con x = 0, queda R = L1, y los puntos entre los que se mide la distancia resultan ser el vértice superior y el inferior derecho.
b) con x = 1, aplicando el teorema del coseno al interior de la raíz, queda R = L3. Ahora los puntos extremos son el vértice superior y el inferior izquierdo.

En cambio, si w = 0, resulta que R = 0 para cualquier valor de x. Eso significa que hemos extraído, o factorizado, un cero de la raíz.
Al estar factoreada, esta variable w se puede cancelar con otro factor w (el jacobiano de la transformación) que aparece en el numerador, así la integral puede calcularse sin problemas.

El tema clave es probar que para cualquier valor de x, la raíz no se anula nunca.
Si se anulara estaríamos fritos, porque significaría que aún no hemos extraído todos los ceros del denominador !
Entonces buscamos los valores que anulan el corchete y, luego de algunos reemplazos, dan:

x(1,2) = - (L1/L2) [cos [LATEX]a[/LATEX] ± √ (cos²[LATEX]a[/LATEX] - 1)]

¿ Alguien se anima a interpretar éste resultado ?

Bueno, una ayuda: el resultado es una distancia, y por lo tanto debe ser un número real y positivo.


PD: Casos intermedios para x y para w.
Cuando x = constante y w recorre el rango 0->1, se dibuja una recta que va del vértice superior hasta algún punto sobre L2.
Cuando w = constante y x recorre el rango 0->1, se dibuja una recta paralela a L2 que corta ambos lados L1 y L3.

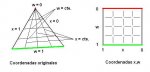
La transformación de Duffy es similar al paso de coordenadas "cartesianas" a "polares", sólo que en lugar de "polares" se tienen coordenadas "triangulares": w=const. no es un arco, como ocurre en polares con radio=const.
El punto cartesiano w=0, luego de la T. de Duffy se convierte en un segmento de largo 1, y en eso consiste remover la singularidad.

 

[foso]

Hola Asherar. Interesante lo que publicas. Es un tema que me intriga, el calcular la impedancia de las antenas. Ahora mismo estoy emezando a laburar con bluetooth, y si bien ya están hechos los modelos de antenas y hay muchos, está bueno entender algo del cálculo.
Una pregunta ¿conocés algún libro donde haya sobre lo que exponés ahi?



Ya que creaste este post y veo que te gusta la matemática, voy a aprovechar a publicar algo que estoy inventando. Es probable que cuando lea esto un moderador me lo limpie o usuarios hagan comentarios despectivos. De todos modos lo publico para que me ayuden a crearlo y modificarlo o bien para que me hagan entender que no vale la pena porque no serviría. Se trata de un juego al que llamé "Polos y Ceros" . La mejor forma de saber si sirve es jugarlo con alguien. Es mas o menos asi:

Cada jugador cuenta con un sistema realimentado y un mapa zero-polar independiente con límites en (+-5, j+-5). Como muestra la figura de ejemplo.

La transferencia de realimentación de su sistema vale H(s) = 1. Y la planta con la que comienzan ambos es G(s) = 1/(s+1).

El lugar de raices de los sistemas de ambos jugadores es público (ambos pueden verlo). A medida que vaya cambiando su sistema el jugador debe ir actualizando su lugar de raices, con la supervisión del contrario.

Objetivo: gana el juego el que llega a tener un sistema con 3 polos estable.

Procedimiento:

Cada jugador dispone en su mapa zero-polar 10 polos y 10 ceros en donde quiera, sin mostrarle al oponente, los lugares posibles son números enteros y las singularidades complejas deben ir apareadas. No se permiten singularidades múltiples.

Luego se procede parecido a la batalla naval. El jugador que comienza elige una posición en el mapa del otro y dice: "polo" o "cero" en "tal lugar". Por ejemplo: "un polo en 3 + j".
Se irán alternando los disparos. El que comienza segundo debe ser el último en disparar al finalizar el juego.
Nunca se podrá tener mas de 3 polos o mas de 3 ceros en cada sistema.

Hay 3 diferentes casos:

1) Si el jugador acierta la posición de un polo. Ese polo se le añade al sistema DEL CONTRARIO. Si el contrario ya tiene sus tres polos, deberá cambiar la poscion de alguno (según su elección) a la del nuevo polo.

2) Si el jugador acierta la posición de un cero. Ese cero se la añade a SU sistema. Si el jugador ya tiene sus tres ceros, deberá cambiar la posición de alguno (según su elección).Además el jugador contrario tiene la opción de añadirlo al suyo o no.

3) Si el jugador acierta la posición pero no el tipo de singularidad, se invierte el signo de realimentación de su sistema.

 

[asherar]

Fosoooooooooooo ... ¡ me volaste la percoca (cabeza) !
¿ Y por qué te lo van a borrar ? Si está re-grosso !!!

Todavía no entendí muy bien como es la ideosincracia del juego, pero se promete muy extravagante.
Dame un tiempo para repasar la teoría y luego jugamos una partida.
Hasta se podría pensar en una interfaz interactiva para jugarlo en red, con alguna estética bien "matematicosa".

Como sabrás, Matlab tiene toda una biblioteca de funciones para este tipo de cosas: root-locus, función de transferencia, etc.


Lo que yo hago es calcular las corrientes inducidas en superficie cuando incide una onda de radar sobre un objeto metálico. Para eso se calcula la matriz de impedancias Z de la superficie, correspondiente a la frecuencia f del campo incidente E. Luego, se resuelve una ecuación matricial del tipo Z J = E, donde J es la corriente solución incógnita. Una vez obtenida J, lo que sigue es calcular el campo eléctrico dispersado por esas corrientes, y de ahí la sección eficaz de radar.
La superficie dispersora se desarrolla como un poliedro de caras triangulares, y la cantidad de aristas determina la dimensión N del problema: Z es matriz de NxN, J y E son vectores de N elementos.
Para calcular el campo dispersado en cualquier punto se usa el método de campos retardados, igual que para el cálculo de lóbulos de emisión.

Sobre el cálculo de antenas, hay algunas cosas descargables en internet, pero como casi siempre ocurre, lo interesante no lo encontrás por ningún lado.
Por ejemplo, vas a encontrar artículos de las funciones de Rao-Wilton-Glisson, que se usan para desarrollar la corriente superficial, pero la teoría de la Transformación de Duffy no existe en internet.
La teoría la tuve que desarrollar paso a paso a partir de las ecuaciones de Maxwell, para estar seguro de cada punto y coma. No me podía arriesgar a tomar una fórmula final sin saber de dónde viene cada cosa. Pero la remoción de la singularidad en las integrales lo tuve que estudiar a partir de un artículo científico que me consiguió un colega en la universidad (me ahorró 39.- U$D).
Mensaje para los "amigos de la erudición": hay cosas que no están en los libros !!!

 

[asherar]

Análisis de la solución:

x(1,2) = - (L1/L2) [cos

± √ (cos²

- 1)]

Para que x sea real debe ocurrir que la expresión dentro de la raíz debe ser positiva.
Como el cuadrado del coseno de cualquier ángulo es siempre menor o igual que uno,
entonces, los únicos resultados posibles corresponden a ángulos de 0º y de 180º.
Esto hace que la raíz cuadrada sea nula, y que x sea un número real.

Para que x sea positivo se requiere además que el coseno sea negativo, a fin de cancelar
el signo escrito. Esto decide que el ángulo debe ser de 180º.

Debido al rango de 0 <= x <= 1 se concluye que 0 <= L1 <= L2.

Por lo tanto los tres lados se encontrarán alineados. Un triángulo de estas características se denomina degenerado, y tiene área nula (no es un triángulo).
O sea que el denominador de la integral se anula cuando el dominio de integración no corresponde a un triángulo. Como la malla de cálculo está formada por triángulos, es como decir que el denominador no se anulará nunca.
Para evitar un resultado indeseado en el denominador, al construir la malla de triángulos deberemos asegurarnos que ninguno sea degenerado, incluso demasiado alejado del equilátero.

Triángulos que se acerquen a este comportamiento "degenerado" también ocasionarán problemas. El valor del denominador, aunque no sea nulo, también originará resultados finales con valores elevados.
Esto puede parecer normal, pero el efecto concreto es que aumentará el error de los cálculos.

Para comprobar ésto veamos como ejemplo el cálculo del área.
Si el triángulo es casi-degenerado podemos calcular el área de la mitad derecha A1 como:

A1 = (1/2) L1 . d

La cota del error relativo de A1 es la suma de los errores relativos de L1 y d:

E(A1) = E(L1) + E(d)

Si d es cercana a cero, su error relativo será del 100%, entonces: el error relativo de A1 tambien será cercano al 100%.
Lo mismo ocurre con A2 = (1/2) L2 . d.

 

[asherar]

Estaba pensando con respecto al juego que propone foso, que cada jugador podría disponer de información
del adversario en forma "borrosa", como por ejemplo: saber el módulo de las raíces o polos pero no la fase. O al contrario. De esta forma el juego se haría algo más deductivo aunque igualmente azaroso.
...
Son ideas.
Que no decaiga !

 

[asherar]

Redondeo inocente y redondeo catastrófico.

El redondeo de las operaciones algebraicas se lleva a cabo tratando de que el error generado tenga características pseudo-aleatorias (redondeo simétrico). Esto es que el 50% de los redondeos causen
error por exceso y el otro 50% causen error por defecto.
Si esto fuera exactamente así, el resultado acumulativo sería que los errores de redondeo tenderían a cancelarse no representarían un problema.
Tal vez por ese motivo el error de redondeo no suele tenerse en cuenta al calcular la propagación de errores en unas pocas operaciones, o en operaciones aisladas.

La cosa cambia notablemente cuando la cantidad de operaciones crece a cantidades realmente grandes,
(miles de millones de cuentas) como ocurre en simulaciones numéricas de procesos de todo tipo.
El resultado del acarreo de estos errores puede ser catastrófico, como se puede ver en estos ejemplos.

* 25 de Febrero 1991. Falla en el sistema de defensa Patriot (Irak) Reporte GAO/IMTEC-92-26.
Problema de software razón acumulación de errores de redondeo.
(www.math.psu.edu/dna/455.f97/notes.html)

* 4 de Junio 1996. El cohete Ariane 5 se auto destruye la corto tiempo del despegue. Causa del desastre
un error de overflow. (ver el mismo enlace anterior, segunda parte)

* 1997 un error de redondeo es descubierto en los procesadores Pentium-II. Problema no solo de imagen
de la empresa (INTEL) sino el costo del reemplazo de un gran numero de procesadores defectuosos. (x86.ddj.com/secrets/dan0441.htm ** enlace roto **)

* Por un error informático se calculan mal los dividendos de las acciones resultando cifras astronómicas.
( ... no haber comprado antes !!!! )