Disculpen tengo una duda... mi profesor de fisica... mientras nos enseñaba ley de ohm, nos presento un problema como trabajo para la casa... y quisiera saber si me pueden ayudar a resolverlo y me explican como resolverlo porfa...
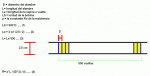
Una bobina de laboratorio de 10Ohm de resistencia es de forma cilindrica, de 2,5cm de diametro. Si la bobina esta compuesta de 500 espiras de alamrbre de cobre. Calcular el tamaño de la bobina.
espero que puedan ayudarme... Desde ya muchisimas gracias...
Una bobina de laboratorio de 10Ohm de resistencia es de forma cilindrica, de 2,5cm de diametro. Si la bobina esta compuesta de 500 espiras de alamrbre de cobre. Calcular el tamaño de la bobina.
espero que puedan ayudarme... Desde ya muchisimas gracias...