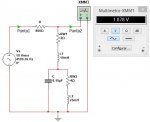
Hola chicos, aquí con una nueva duda. Resulta que debo calcular el voltaje de salida (sin carga) del circuito serie-paralelo con una frecuencia de 4109.36Hz, y acorde a la solución del libro del ejercicio, mi cálculo me da un resultado totalmente distinto. Y si bien mi análisis se me hace bien lógico, no puedo llegar al resultado correcto (he llegado a creer que hasta el libro está mal jajaja).
Este es el circuito:
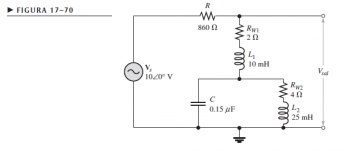
El método que estoy utilizando es mediante numeros complejos y mostrar el resultado fasorialmente, ya que necesito el ángulo del mismo voltaje de salida también. Simplemente calculo la impedancia de L2 y RW2 en serie, la cual está en paralelo con C. Así formo con los 3 elementos una impedancia equivalente, la cual sumo en serie con L1 y RW1. Así obtengo la impedancia de toda esa red. Luego calculo el voltaje de la red con:
VSalida = ((ZRed) / ZRed + R) * VS;
Acorde a los resultados del libro, a la frecuencia 4109.36Hz, me debería dar un voltaje de salida de 4.83<-61º V, pero actualmente me está dando 1.95463<-77.4736º V.
Les agradezco de antemano!
Adjunto también el código del script en Matlab:
Este es el circuito:

El método que estoy utilizando es mediante numeros complejos y mostrar el resultado fasorialmente, ya que necesito el ángulo del mismo voltaje de salida también. Simplemente calculo la impedancia de L2 y RW2 en serie, la cual está en paralelo con C. Así formo con los 3 elementos una impedancia equivalente, la cual sumo en serie con L1 y RW1. Así obtengo la impedancia de toda esa red. Luego calculo el voltaje de la red con:
VSalida = ((ZRed) / ZRed + R) * VS;
Acorde a los resultados del libro, a la frecuencia 4109.36Hz, me debería dar un voltaje de salida de 4.83<-61º V, pero actualmente me está dando 1.95463<-77.4736º V.
Les agradezco de antemano!
Adjunto también el código del script en Matlab:
Código:
% Se limpia.
clear;
clc;
% Valores componentes.
v = 10;
r = 860;
l1 = 10e-3;
rw1 = 2;
l2 = 25e-3;
rw2 = 4;
c = 0.15e-6;
% Frecuencia resonante del circuito RLC en serie L1-C
fr1 = 1 / (2 * pi * sqrt(l1 * c));
% Reactancias.
xl1 = 2 * pi * fr1 * l1 * 1i;
xl2 = 2 * pi * fr1 * l2 * 1i;
xc = (1 / (2 * pi * fr1 * c)) * -1i;
% Impedancias equivalentes.
zl1 = rw1 + xl1;
zl2 = rw2 + xl2;
zl2c = 1 / ((1 / xc) + (1 / zl2));
% Impedancia de la red.
zrama = zl1 + zl2c;
ztotal = r + zrama;
% Voltaje de salida.
vsalida = (zrama / ztotal) * v;
fprintf('Frecuencia resonante: %g Hz\n', fr1);
fprintf('Impedancia de rama: %g<%gº ohms\n', abs(zrama), radtodeg(angle(zrama)));
fprintf('Impedancia total: %g<%gº ohms\n', abs(ztotal), radtodeg(angle(ztotal)));
fprintf('Voltaje de salida: %g<%gº V\n', abs(vsalida), radtodeg(angle(vsalida)));