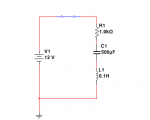
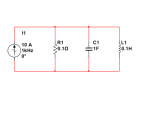
En el circuito adjuntado, para calcular la corriente del transistorio se plantea la ecuación diferencial y se llega a la siguiente expresión:
i(t)=C1 e^(-2t) + C2 e^(-9998t) (1)
Para calcular las constantes C1 y C2, se plantea que en el tiempo inicial la corriente es cero
0= C1+C2
¿Eso es debido a la oposición al cambio de corriente que presenta la inductancia?
Luego se plantea que en el instante cero, todo el potencial es aplicado a la inductancia
V=L [di(t) / dt] (2)
entonces [di(t) / dt] = V/L
se deriva la expresión (1) y se despeja una constante y luego se resuelve el sistema.
En ese caso ¿se plantea (2) ya que como la inductancia se opone a la corriente toda la tensión cae sobre esta?
Saludos.
i(t)=C1 e^(-2t) + C2 e^(-9998t) (1)
Para calcular las constantes C1 y C2, se plantea que en el tiempo inicial la corriente es cero
0= C1+C2
¿Eso es debido a la oposición al cambio de corriente que presenta la inductancia?
Luego se plantea que en el instante cero, todo el potencial es aplicado a la inductancia
V=L [di(t) / dt] (2)
entonces [di(t) / dt] = V/L
se deriva la expresión (1) y se despeja una constante y luego se resuelve el sistema.
En ese caso ¿se plantea (2) ya que como la inductancia se opone a la corriente toda la tensión cae sobre esta?
Saludos.