Hola a todos, la propuesta que más adelante haré es para aquellos del foro que estén interesados en participar en el diseño y prototipado de uno (o varios) sistemas de codificación estéreo y RDS para emisoras de FM. EL objetivo es primero diseñar la parte del encoder estéreo y una vez tengamos un diseño que cumpla con las pretensiones, incorporarle un sistema RDS. Estoy seguro que parte de los bloques del encoder estereo pueden usarse también para el encoder RDS por lo que ahorramos recursos a la hora de implementar ambos enconders al mismo tiempo.
De antemano aviso que el post es un bastante largo, pero seguro que algunos lo vais a encontrar interesante… Habrá premio para los que lean hasta el final, jejejeje.
Llevo dándole vueltas a este asunto desde hace tiempo ya que los sistemas que he visto implementados siempre tienen algún punto débil:
O bien son caros (DACs de muy alta velocidad y CPUs), o no son de calidad para emisión en broadcast (como los que usan los IC monoliticos tipo BH1417, BA1404, etc), o muy inestables y difíciles de ajustar (MC1496), o no funcionan bien en todos los receptores FM (fallo de precisión en la subportadora de 38kHz).
De los que más me han gustado ha sido el de Pira.cz (http://pira.cz/eng/stk2en.htm), pero hay cosas que no me gustan de él. Lo que menos me gusta es la desviación de la portadora de 38kHz de unas cuantas decenas de hercios por no usar un cristal que sea múltiplo exacto de dicha frecuencia, que puede que para la mayoría de receptores funcione aceptablemente bien, pero para algunos falle la decodificación, en especial en los receptores baratos tipo SDR (algunos sólo sincronizan la fase de la piloto pero no ajustan la frecuencia sino que sintetizan directamente mediante FFT la portadora de 38.000kHz), que cada día son más comunes de encontrar en teléfonos móviles, aparatos de mp3/mp4, etc. Además pienso que el de Pira desperdicia recursos aunque obtiene buenas prestaciones. Pienso que es posible hacer algo de la misma calidad con elementos más sencillos (por ejemplo un MCU más económico)
De los basados en la multiplexación directa usando una cuadrada de 38kHz y dos switches tipo 4066 casi no hablo ya que padecen de todos los males, mucho fondo de ruido a causa de la cantidad de armónicos en la conmutación que no pueden terminar de filtrarse al estar muy cercanos a la banda pasante y una separación de canales muy pobre, alrededor de unos 15-20dB debido a la falta de compensación de niveles y falta de ajuste de la fase de la piloto, una vez senoidificada, con respecto a la subportadora.
Así que el primer objetivo es hacer un codificador económico, lo más preciso posible (como mucho 10Hz/20Hz de desviación con respecto a la portadora de 38kHz, y si es menor pues mucho mejor, ya que por encima de los 20Hz de desviación en algunos receptores se produce un efecto cacofónico familiar a aquellos que tienen receptores SSB). Deseable que tenga buen margen SNR, de 60dB si es posible, y una separación de canales acorde al SNR. Si tienes un margen SNR de 60dB no vale la pena conseguir una separación de canales mayor a 60dB ya que todo lo que quede por debajo de ese nivel quedará enmascarado por el ruido de fondo.
Esto obliga a utilizar un cristal de cuarzo que sea múltiplo entero de la portadora de 38kHz, de lo contrario estaríamos obligados de usar un PLL/Prescaler/Divisor de ratio de frecuencias, etc, y eso encarece mucho el proyecto. Además antiguamente era difícil conseguir cristales exactos pero hoy día con Internet y por el hecho de que los sistemas baratos también los usan, no es tan difícil conseguirlos.
De hecho este es un proyecto de diseño que tenía aparcado hace tiempo y que ha revivido gracias a que por casualidad hace unas semanas me encontré con una oferta de cristales 4.864MHz muy interesante y los acabé comprando. Con ellos he empezado a hacer mis primeras pruebas.
Estos cristales por lo que tengo entendido son muy difíciles de conseguir pero dan la ventaja de proporcionar un múltiplo de 38kHz que es exactamente una potencia de 2, es decir 128*38kHz = 4.864MHz. Lo que significa que dividiendo por 2^7 la frecuencia del cristal obtenemos la frecuencia de la portadora, y dividiendo por 2^8 tenemos la frecuencia piloto.
También he conseguido cristales de 4.332MHz. Esta frecuencia no es un múltiplo que solo contenga potencias de dos, pero tiene algo muy interesante… Contiene una potencia de 3 de 19kHz, lo que permite conseguir la portadora de 57kHz para el RDS además de la de 38kHz y la piloto de 19kHz.
Resumiendo, con el cristal de 4.864MHz se facilita el diseño de un codificador estéreo aunque se complica ligeramente la construcción del RDS (al no ser el cristal múltiplo de 3). Sin embargo con el de 4.332MHz se complica ligeramente el codificador estereo pero la portadora para RDS se obtiene fácilmente.
Además estoy a la espera de que me lleguen cristales de 38kHz y de 7.600MHz. Estos cristales aunque con ciertos inconvenientes, también son múltiplos enteros de 38kHz (1*38=38 y 200*38=7600) y usando algunas ideas pueden implementar codificadores de mayor calidad que para los que se usan tanto (estos cristales son bastante comunes de encontrar cuando se busca un poco por Internet, ya que son los que se usan para los codificadores monolíticos BA1404 (38kHz) y BH1417 (7.6MHz)).
Resumiendo. Lo diseños deberían estar orientados en utilizar uno de estos cuatro cristales (si encontráis otro posible cristal de una frecuencia múltiplo de 38kHz y que sea accesible de conseguir decidlo porque yo no lo he encontrado):
7.600MHz (Muy accesible y barato, estéreo no trivial, RDS no trivial).
4.864MHz (Raro, estéreo trivial, RDS no trivial).
4.332MHz (Menos raro, estéreo no trivial, RDS trivial).
38kHz (Relativamente accesible, no es caro, estéreo no trivial, RDS no trivial)
Bueno, yo he comenzado haciendo pruebas con el de 4.864MHz aunque he generado también una portadora estable de 38.000KHz usando el de 4.332MHz. Cuando me lleguen los otros cristales haré pruebas con ellos.
Comenzamos con la teoria:
Para aquellos que todavía no tengan claro cómo construir matemáticamente una señal MPX para FM a partir de dos canales de audio, no me voy a extender mucho ya que en estos enlaces lo explica mejor de lo que puedo explicarlo yo…
http://es.wikipedia.org/wiki/FM_estéreo
http://transmitters.tripod.com/stereo.htm
Pero voy a resumir toda la teoría anterior en la típica fórmula para obtener la señal multiplex:
MPX= (Vi+Vd) + (Vi-Vd) * S(38kHz) + 0,1 * P(19kHz)
Donde S es la subportadora senoidal de 38kHz y P la señal piloto de 19kHz. Vi es la señal de audio de canal izquierdo y Vd es la señal de audio del canal derecho.
La señal piloto no interviene en el proceso de codificación sino que se añade al 10% con el fin de servir para sincronizar la subportadora estereo. Así que para simplificar pondremos la señal MPX como :
MPX= (Vi+Vd) + (Vi-Vd) * S = A+B * S
En el receptor, se demodula B=(Vi-Vd) y se filtra A=(Vi+Vd) de esa forma se obtienen dos canales por separado, uno suma (A) y otro resta (B). De hecho el canal Vi se recupera sumando ambas señales (se cancela Vd), obteniendo 2*Vi, y el canal Vd se recupera restando ambas señales (se cancela Vi), obteniendo 2*Vd.
De cómo de balanceados se encuentren los niveles de A=(Vi+Vd) con respecto a B=(Vi-Vd), tanto en amplitud como en fase, dependerá la separación de canales. Esto significa que si por ejemplo el Vi de A no es el mismo exactamente que el Vi de B, en el receptor no se podrá cancelar Vi por completo al restar B de A y por lo tanto en el canal Vd aparecerá una parte del canal Vi, y viceversa, haciendo que la separación entre canales se resienta.
Por lo tanto, para un buen codificador estéreo necesitamos tres cosas:
-Hacer que los niveles Vi y Vd de la señal A sean los mismos que los niveles Vi y Vd de la señal B.
-Hacer que la señal piloto de 19kHz esté exactamente en fase con la de 38kHz.
-Que las condiciones anteriores no varíen con las condiciones de funcionamiento, temperatura, humedad, etc.
Mediante un codificador casi analógico, usando operacionales para generar las señales suma A (Vi+Vd) y resta B (Vi-Vd), y luego utilizar un modulador balanceado para conseguir una multiplicación en cuatro cuadrantes (es decir tanto voltajes negativos como positivos) como el MC1496 para generar la señal B*S, se consigue una separación muy elevada. Lamentablemente las condiciones de estabilidad duran poco ya que al variar los valores de los componentes con el régimen de funcionamiento enseguida sufre la separación de canales, lo que obliga a reajustar de nuevo las condiciones de funcionamiento.
La señal MPX de la fórmula anterior la podemos componer de forma equivalente de esta otra manera:
MPX = Vi * (1 + S) + Vd * (1 – S)
El paso de una fórmula a la otra es muy sencillo matemáticamente ya que sólo hay que operar con un poco de álgebra y recordar propiedades de la suma y la multiplicación.
Parece que ahora la forma de genera la señal se ha complicado al aparecer dos multiplicaciones en lugar de una, pero lo que hay entre los paréntesis, gracias a que suman el 1, y la señal S es una senoidal (la señal S varía entre 1 y -1), nunca valdrá menos de 0, de hecho valdrá entre 0 y 2. Esto hace que los multiplicadores sean de dos cuadrantes en lugar de cuatro, lo que es más fácil de conseguir. Hay un momento en que MPX vale 2*Vi+0*Vd= 2*Vi y otro momento, 180 grados de desfase, o lo que es lo mismo para 38kHz, unos 13,16 us después, MPX será 0*Vi+2*Vd= 2*Vd.
Consideramos que la señal MPX está compuesta por dos subseñales, MPXd y MPXi, que serían:
MPXi = Vi * (1+S)
MPXd = Vd * (1-S)
Y entonces MPX=MPXi+MPXd+0,1*Piloto.
Esta otra forma de expresar la señal MPX sugiere que tanto el canal Vi como Vd se van alternando paulatinamente en el tiempo. Sin embargo en un determinado momento intermedio no se tiene sólo Vi o Vd sino una combinación de ellos.
Por ello se han utilizado técnicas semidigitales para crear las multiplicaciones de (1+S) y (1-S) para los Vi y Vd con el fin de lograr una aproximación de MPX. Digo aproximación porque estas técnicas tratan de conseguir una S que se parezca a una senoidal en mayor o menor medida, pero siempre habrá algo de diferencia entre la señal digital creada por el codificador y la señal senoidal pura S.
El enfoque para un modulador económico es el uso de una señal C en lugar de la S que en lugar de ser Senoidal se aproxima por una Cuadrada que oscila entre +1 y -1. De hecho la señal (1+C) es una señal que vale 2 entre 0º-180º grados y 0 entre 180º-360º. La señal (1-C) será una señal desfasada 180º con respecto a la anterior, por lo que vale 0 entre 0º-180º y 2 entre 180º-360º.
Ya que las señales MPXd y MPXi se generan de la misma forma, con la portadora de 38kHz desfasada 180º, podemos considerar sólo los aspectos de la generación de la señal MPXi (portadora del canal izquierdo) que serán recícprocos en la generación de la portadora del canal derecho, o MPXd.
La multiplicación Vi *(1+C) se consigue fácilmente haciendo que entre 0º-180º ese valor sea 2*Vi, y entre 180º y 360º ese valor sea 0. Con el canal Vd de manera recíproca, entre 0º-180º será 0 y entre 180º-360º será 2*Vd.
Sin embargo, cuando obtenemos MPXi = Vi * (1+C), ya que C es una onda cuadrada de amplitud 1, esta se compone por una serie de fourier de infinitos armónicos impares de senoidales S, que quedan de la siguiente forma:
MPXi = Vi * (1+ 4/PI*(S+1/3*S(3)+1/5*S(5)…)
Esto es algo que no se parece especialmente mucho a la forma original MPXi = Vi*(1+S).
Donde S(3), S(5),... son los armónicos impares de la fundamental que componen la portadora cuadrada.
Si no se eliminan por completo estos armónicos, en el receptor ocurre un fenómeno de aliasing haciendo que aparezcan tonos fantasmas y artefactos en la señal audible que no deberían estar ahí, por lo que el SNR se resiente muchísimo y la calidad del audio se degrada bastante.
Para ello, es necesario un filtro que no distorsione la fase de la banda pasante y sea tan abrupto para eliminar a partir del tercer armónico, o es decir, que deje pasar hasta los 53kHz sin modificar la fase, pero anule al máximo las frecuencias de 95kHz en adelante. Esto es muy difícil de realizar por lo que los codificadores estereo que usen una cuadrada para generar las señales MPXd y MPXi tienen que elegir entre un SNR pobre o una separación pobre, dependiendo si filtran con un filtro muy abrupto que distorsione la fase o con un filtro menos abrupto que distorsione menos la fase pero deje pasar una parte de los armónicos.
Para complicar el asunto más, imaginemos que mediante un filtro ideal que corta a los 53kHz, eliminamos los armónicos S(3), S(5),… En ese caso obtenemos una señal
MPXi = Vi * (1 + S *4/PI)
Lo que hay entre paréntesis debería oscilar senoidalmente entre 0 y 2, sin embargo como S vale como máximo 4/PI y como mínimo -4/PI, lo que hay entre paréntesis acaba valiendo un valor máximo de 2.273 y un valor mínimo de -0.273…
Es decir, que el momento en el que la señal Vi debería valer 0, vale -0.273. Esto implica que la señal compuesta, MPX el instante en el que debería estar sólo presente Vd, es decir, 0*Vi+2*Vd en realidad hay esto: -0.273*Vi+2.273*Vd. Lo que significa que un 12% del canal Vi interfiere en el canal Vd y por lo tanto la separación máxima que podemos conseguir eliminando todos los armónicos es de -20Log(0.12)= 18,41dB. Una separación muy pobre.
Para mejorar esta separación, da igual cuanto valga MPXi en su valor máximo (ya que podemos variar su valor con un control de ganancia, tenemos que hacer que en su valor mínimo sea 0. Para ello a la señal completa se añade esto:
MPX(final)=MPX(filtrada) + (4/PI-1)*(Vi+Vd) =>
MPXi = Vi * (4/PI + S * 4/PI )= Vi * (1+S) *4/PI
Ahora aunque está el factor 4/PI, lo importante es que la señal que varía, es decir, lo que hay entre el paréntesis, va entre 0 y 2 por lo que MPXi valdrá entre 0 y Vi*2*4/PI.
Esto se traduce en que si implementamos un multiplexor que alterne las señales Vd y Vi, a la salida de ese multiplexor se debe de sumar un 27’3% de la señal suma (Vd+Vi) y de esa forma aumentamos considerablemente la separación de canales. Tristemente casi ninguna implementación de este tipo que utiliza switches tipo 4066 añade esta compensación.
Aquí se muestra gráficamente lo que se ha explicado:

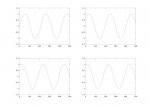
En la figura 1, se ve la señal Cuadrada que es la que se usa para multiplicar Vi, y la señal teórica S que tendría que variar entre 0 y 2. En la figura 2 se tiene la señal cuadrada original, y la señal senoidal REAL que resulta tras filtrar el tercer y sucesivos armónicos. Notar el pico negativo de dicha senoidal. En la figura 3 se nota la onda cuadrada compensada sumándo un nivel de 0,273 *Vi, y la onda senoidal resultante que en ningún caso acaba estando por debajo de cero.
Pero aunque podamos compensar los niveles de señal, tenemos el problema de encontrar un filtro que elimine completamente el tercer y sucesivos armónicos y deje intacta la fase de la banda pasante. Por ello lo que sustituya a la senoidal S en la ecuación, no puede ser una simple cuadrada sino tiene que ser algo más.
En mis diseños usaré varias ideas para sintetizar la señal S con un mínimo de calidad que permita utilizar un filtro no tan abrupto pero que respete la fase, y al mismo tiempo la compensación, si es que es necesaria, sea menor que en el caso de la onda cuadrada.
Lo más lógico es que no necesitemos eliminar el armónico S(3) porque en la onda que utilicemos ese armónico no exista. Podemos usar un sistema para cancelar el tercer armónico de la señal que usemos para imitar S. Pongamos que tenemos la onda cuadrada C que hemos usado antes. Ahora la hacemos pasar por un retardo que a su salida muestre la misma señal C pero con un desfase de 60º. El tercer armónico tendrá un desfase de 60*3=180º, es decir tendremos –S(3). Si ahora sumamos esta onda con la onda original, el tercer armónico de la onda resultante sera S(3)+(-S(3))=0. Esa misma onda la dividimos por 2 para recuperar los niveles originales. De esa manera tenemos una onda M (cuadrada modificada o senoidal modificada) que recordará a la cuadrada original, pero que carece del tercer harmónico. Además el proceso se puede repetir desplazando nuevamente primero por 36º y depués por 25,71º para anular el armónico 5 y 7. El armónico 9 se anuló al anular el tercer armónico ya que el armónico 9 es múltiplo de 3. Una cuadrada que se ha retardado 3 veces y se ha promediado otras tantas veces acaba siendo una onda que contiene sólo 9 niveles (suficiente para ser generado con un DAC de 4 bits) y su primer armónico es el número 11 (es decir, en 418kHz, ya muy alejado de la banda que nos interesa y por lo tanto fácilmente filtrable sin alterar la fase de la banda pasante).
Aunque la señal sólo tiene 9 niveles, una vez filtrados por completo los armónicos restantes, no tenemos una señal de resolución 4 bits. Tenemos una señal senoidal pura (que habrá que compensar ya que siempre que quedan armónicos hay que compensar algo pero muchísimo menos que con la cuadrada original).
En la imagen siguiente se muestra el proceso de ir quitando armónicos promediando esa misma cuadrada con ella misma desfasada, y repitiendo varias veces para distintas fases…
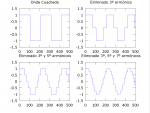
De hecho este sistema de eliminación de armónicos por interferencias se le conoce como filtro peine (ya que no sólo elimina un armónico si no que todos sus múltiplos, haciendo ver que la respuesta del filtro se parecer a un peine) y funciona con cualquier forma de onda de entrada.
A modo de ejemplo se incluyen ondas modificadas eliminando armónicos donde en lugar de una cuadrada tenemos una triangular, y una parabólica.
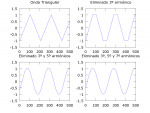
Pero tomemos otra vez la onda modificada a partir de la cuadrada (que es más fácil de multiplicar que la triangular o la parabólica ya que la cuadrada sólo tiene dos estados).
Ahora supongamos que implementamos una cuadrada de 38kHz y la desfasamos 60º. Esas dos señales las usamos para multiplicar Vi de forma que generamos la siguiente expresión:
MPXi=Vi * (1+M)
Donde M ahora es 2*sqrt(3)/PI* (S+1/5*S(5)+1/7*S(7)…). Ahora vemos que ya no existe S(3) y los armónicos comienzan en S(5) que es el de 38*5=190kHz. Ahora ya es mucho más fácil filtrar esos armónicos ya que podemos usar un filtro que no sea tan abrupto y conserve mejor la fase. Si ahora filtramos, tenemos que nos queda el factor 2*sqrt(3)/PI =1,103:
MPXi=Vi * (1 + S * 1,103), es decir, que sin compensar hemos disminuido el crosstalk de un 12% a un 4,9% lo que da una separación de 26,3dB. No es un gran logro, pero son 8dB más que con la onda cuadrada. Además sólo hay que compensar con un 10.3% de la señal suma en lugar del 27,3% del caso de la onda cuadrada.
En la imagen siguiente se ven las figuras de antes pero ahora aplicadas a una onda modificada para eliminar el tercer armónico

Lo ideal sería poder implementar varios filtros con varios desfases para poder anular hasta el armónico 7, como se ha mostrado en las imágenes de más arriba, pero de forma analógica cuantos más desfasadores más fácil que alguno se vaya de fase por lo que acabamos teniendo otra vez niveles de armónicos que no filtra el filtro de salida. Sin embargo podemos utilizar un sobremuestreo digital para generar la señal senoidal exacta sin armónicos hasta el número 11. Esto requiere que la frecuencia de conteo sea un múltiplo de dichos armónicos para que al dividir por esas cantidades la frecuencia sea exacta, es decir, la frecuencia original tiene que ser múltiplo de 3, de 5 y de 7, lo que hace que deba valer x105. Lamentablemente no podemos conseguir el cristal necesario para poder alcanzar un sobremuestreo de x105, ya que el valor del cristal debería ser de 3.990Mhz. Alguien podría pensar que se podría usar un cristal de 4MHz y santas pascuas, ya que casi casi se llega a tener a 4MHz pero al dividir por 105, la frecuencia resultante sería de 38,095kHz, lejos de nuestra pretensión de conseguir los 38,000kHz exactos.
Sin embargo si sólo queremos eliminar “digitalmente” el armónico tercero ya que disponemos de un filtro decente para eliminar el quinto y sucesivos, lo podemos hacer relativamente fácil utilizando un cristal de 4.332kHz (ya que es múltiplo de 3), disponible fácilmente y de paso ya obtener la señal de 57kHz para alimentar un enconder RDS.
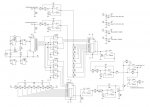
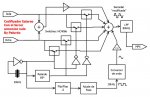
Aquí os propongo dos sistemas para lograr codificar mediante una onda modificada para elimnar el tercer armónico. El primero genera una cuadrada a 38kHz mediante un cristal de esa frecuencia, y una red de desfase genera una señal desfasada 60º (el desfasador puede ser una red RC que retrase la cuadrada durante 4,4 us y un trigger schmitt que vuelva a conformar la señal en cuadrada. Entonces usamos ambas señales para combinarlas en un sumador obteniendo la multiplicación directa de ambos canales por las señales (1+M) y (1-M). Los restantes bloques no necesitan mucha explicación. Está la red de compensación para anular el crosstalk, y el sistema para generar la señal piloto de 19khz mediante un biestable tipo T y un conformador de onda senoidal (puede ser un filtro en 19kHz con una Q bastante elevada), además de otro retardo para poder ajustar la fase senoidal para minimizar de nuevo el crosstalk.
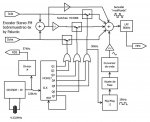
El segundo sistema hace lo mismo que el primero pero las señales desfasadas son generadas por un contador secuencial de 6 estados. Este sistema tiene la ventaja de que por diseño el desfase de 60º no puede variar por las condiciones de funcionamiento, frio, calor, humedad, etc. Por lo demás es igual que el primero, aunque este usa un cristal de 4.332MHz y permite generar además la portadora RDS de 57kHz.
Otro método para multiplexar con una senoidal:
Además de la cancelación de armónicos, es posible sintetizar las señales (1+S) y (1-S) mediante otros métodos. El más utilizado en codificadores con sobremuestreo es el uso de DACs multiplicadores de dos cuadrantes o bien un DAC multiplexado a distintos niveles. El DAC típico es aquel que hace uso de una matriz de resistencias para proporcionar a su salida el nivel analógico proporcional a la señal digital de entrada. Los más conocidos de este tipo son las redes R-2R en escalera, y las resistencias ponderadas (cuando se pretende generar señales periódicas conocidas).
Otro tipo de DACs menos conocidos pero más comunes ya que funcionan casi enteramente en el terreno digital, son los DACs con modulación por densidad de pulso o PDM. No confundir con PWM o modulación por ancho de pulso, que se trata de otra forma de implementar un DAC pero no tan digital… A la modulación PDM también se la conoce por su construcción, como modulación Delta-Sigma (o Sigma-Delta). Un modulador Delta-Sigma lo que hace es rastrear una señal analógica generando pulsos más “juntos” cuanto más alto sea el nivel de la señal analógica. Para una descripción más detallada visitad el enlace de la wikipedia sobre esta modulación:
http://es.wikipedia.org/wiki/Modulación_Sigma-Delta
Una característica de este sistema es que para alcanzar una buena resolución es suficiente con pocos bits siempre que podamos hacer funcionar el modulador mucho más rápido que la frecuencia que queremos sintetizar. De hecho es bastante común ver moduladores Sigma-Delta utilizando solamente un bit.
La característica de este modulador se basa en que los armónicos en lugar de ir desplazándose por igual a lo largo del espectro, se concentran en la parte alta de él, por lo que un sencillo filtro pasa bajo con la frecuencia de corte alejada de la zona donde la densidad de armónicos es mayor, reconstruye fielmente la señal original.
Nosotros no necesitamos la parte ADC, es decir, el rastreador que genera los bits. Podemos generar una tabla de bits que contengan la secuencia Delta-Sigma de una senoidal a una determinada frecuencia, y esa tabla guardarla en una memoria rápida, ya sea una EPROM, una RAM, o un microcontrolador. Sin embargo la parte DAC del modulador, puede ser tan sencilla como un filtro RC con la frecuencia de corte dos décadas por debajo de la frecuencia de muestreo (consiguiendo 40dB de atenuación de los armónicos molestos). Es decir, un simple switch conmutando rápidamente pongamos a 128 veces la frecuencia que se quiere sintetizar, y luego al filtrar obtenemos el canal de audio correspondiente multiplicado con la senoidal (1+S) con una resolución bastante aceptable.
La siguiente imagen muestra las ondas cuando la frecuencia del chorro de bits es de 128 veces la frecuencia de la subportadora, es decir 128*38=4.684MHz. Además fácilmente podemos generar varias ondas a la vez ya que disponemos de varios bits en la memoria por cada posición temporal de la secuencia. Por ejemplo podemos utilizar 1 o dos bits tanto para generar las ondas de 38kHz como la piloto de 19kHz.

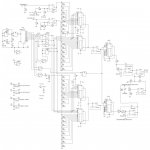
Los siguientes esquemas se basan en este principio. El primero usa una memoria tipo EPROM y un cristal que alimenta el reloj del contador que direcciona dicha memoria. Para generar la señal de 19kHz es necesario repetir 2 veces la de 38kHz, por lo que con un cristal de 4.864MHz hace falta 256Bytes, con uno de 7.6MHz, 400Bytes, y con el de 4.332MHz, 228Bytes. Excepto en el caso del cristal de 4.864MHz, para los otros cristales la posición siguiente a la última de la tabla hace que el contador se resetee y vuelva al principio de la memoria.
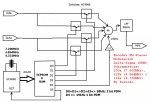
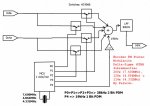
Aunque en estos esquemas no aparece, al eliminar una buena parte de los armónicos, el nivel de la onda fundamental se reduce notablemente, pero no así el nivel de continua. Esto significa que es necesario compensar aunque en este caso en lugar de sumar a MPX la señal (Vi+Vd) hay que restar un tanto por ciento de ella, equivalente al nivel excedente de dicha señal en la señal compuesta final.
Pruebas en protoboard
Para tratar de generar tanto los pulsos a 38kHz y 19kHz como las ondas senoidales correspondientes a esas frecuencias, he probado de momento utilizando la tabla de ondas Delta-Sigma que he generado para construir la gráfica que hemos visto anteriormente. He usado dos bits para codificar la señal de 38kHz PDM de 2 bits, un bit más para codificar la misma señal con resolución de 1 bit, y 3 bits más para generar las de 19kHz de dos bits y la de 1 bit. En total he usado 6 bits de los 8 disponibles en una memoria paralela EEPROM modelo X2804 de Xicor (es lo que tenía por el cajón desastre). Como no son muchos bytes la he programado manualmente.
He usado un cristal de 4.864MHz con una puerta 74HC04 para generar el tren de ondas que alimenta al contador.
Precisamente el problema de mi montaje y el que me ha limitado bastante los resultados ha sido utilizar una versión de baja velocidad del 4040, como es el MC14040 que funciona bien hasta los 2MHz para 5V (le he dado un tren de pulsos de más del doble de rápido). El contador contaba, pero Q1, es decir A0 en la memoria, nunca bajaba de 2,5V por lo que siempre quedaba en 1. El resultado es que con este contador sólo he podido direccional las direcciones impares de la memoria a esa velocidad por lo que el sobremuestreo se reduce de x128 a x64. Además la falta de velocidad hace que las direcciones se arrastren en la serie (van retrasadas con respecto al tren de pulso) lo que hace que la onda resultante no sea perfectamente senoidal sino que se arrastra ligeramente hacia atrás.
Espero corregir estos problemas cuando consiga un 74HC4040 que es 10 veces más rápido que el MC14040.
De momento estas son las imágenes que he ido obteniendo de las pruebas. Aquí muestro una imagen de la parte generadora Delta-Sigma montada en protoboard:

Aquí una foto de la onda cuadrada generada por el cristal:

En la siguiente foto, la salida Q8 del contador (19,000 kHz es decir 4864/256)

En la siguiente foto, la salida Q7 (38,000 kHz es decir 4864/128)

En la siguiente foto, se tiene la señal PDM de 19,000KHz de un bit con respecto al reloj de 19KHz.

En la siguiente foto, se tiene la señal PDM de 38,000KHz de un bit con respecto al reloj de 38KHz.

En la siguiente foto, coloqué un pasabaja RC con una resistencia de 10k y un condensador de 470pF a la salida de cada una de las señales PDM, de 19 y 38kHz. La señal de 19kHz se reconstruye bastante bien a pesar de ser solo de 1 bit, aunque la asimetría se debe al arrastre de bits que he comentado antes por culpa del contador. Sin embargo aunque también debería convertirse bien, la señal PDM de 38kHz aparece formada como si fuera una triangular.

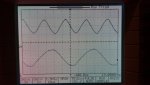
Ya en la última foto, el arrastre de bits para la señal PDM de 19kHz y dos bits de resolución no la puse ya que aunque mejoraba la simetría, una zona presentaba una fuerte distorsión. Sin embargo la de 38kHz si que mejoraba al usar 2 bits (básicamente colocar 2 resistencias de 10k en las dos salidas y unidas en el mismo condensador de 470pF que hace de integrador y sumador de ambas señales). Ahora ya en la de 38kHz se ve sintetizada claramente senoidal.
De momento estas son las pruebas que he hecho. Quiero conseguir más integrados lógicos, como más contadores, flip-flops, más puertas rápidas, etc. Así podré implementar varias versiones de los diseños que he mostrado y ver cual de todos es más estable, genera menos ruido, más separación, es amigable con el RDS, etc.
De ahí el título de este POST. Soy una persona de recursos limitados, y además me gustaría que este proyecto fuera colaborativo y quedara como diseño del foro (luego ya cada uno que hiciera lo que quisiera con él).
Propuesta:
Por ello me gustaría saber si hay gente dispuesta a probar las ideas que he explicado aquí, en definitiva contribuir a concretar algunos de los diseños que he propuesto, ya sea materializando los bloques funcionales o añadiendo más (filtros de pre-énfasis, etc). Y una vez tengamos unos cuantos moduladores estéreo, diseñar el modulador RDS que mejor se adapte al modulador estéreo (usando la frecuencia de reloj maestra por ejemplo).
No es un proyecto que tenga que hacerse rápido, es decir, que me da igual si cuesta un año o más en realizarse, pero si sale algo decente podríamos tener un diseño que se hiciera popular y así dar algo de publicidad al foro.
Como sale más barato comprar cantidad de componentes cuando compras por ebay y otros sitios online, tengo más cristales de los que voy a utilizar.
Dispondría para compartir los siguientes cristales que son difíciles de conseguir, en principio para compartir 1 cristal por persona:
10 cristales de 4.864MHz.
10 cristales de 4.332MHz.
Y en cuanto me lleguen por correo compartiré además los siguientes:
10 cristales de 7.600MHz.
10 cristales de 38kHz.
No cobraría nada por el cristal, lo único que pido sería los gastos de envío que para España sería de 1 euro aproximadamente, y se haría mediante correo ordinario. Para fuera de España en especial para Latinoamérica el envío se multiplica varias veces por lo que en un principio lo ideal sería que participaran foreros españoles, aunque alguien que consiga los cristales por su cuenta o esté dispuesto a pagar los gastos de envio internacionales, bienvenido sea.
Además si alguien necesita más de un cristal, tendría que justificarme por qué quiere más de uno. Tiene que ser también alguien del foro, es decir, alguien que participe activamente. Aunque no tenga muchos mensajes, tiene que tener al menos mensajes que sean relevantes o algún que otro aporte.
Los interesados en un cristal que comenten que quieren participar en el diseño en este mismo hilo.
El diseño debería de comenzarse a concretar o implementar, o por lo menos alguna de sus partes, antes de 6 meses desde la fecha en que envíe el cristal. No importa que después se tarde en terminar el proyecto, lo importante es que al menos empiece.
Bueno, pues espero vuestras ideas y aportes al proyecto, y como no, vuestras solicitudes.
Ahh, si alguien quiere implementar el proyecto utilizando una tabla generada en una memoria RAM de alta velocidad, dispongo de 10 chips de RAM estática HM6116 reciclados de una máquina recreativa. Podría enviar uno de ellos junto al cristal (siempre que el sobre en total no supere los 20 gramos).
Un saludo, y gracias por llegar a leer hasta el final.
De antemano aviso que el post es un bastante largo, pero seguro que algunos lo vais a encontrar interesante… Habrá premio para los que lean hasta el final, jejejeje.
Llevo dándole vueltas a este asunto desde hace tiempo ya que los sistemas que he visto implementados siempre tienen algún punto débil:
O bien son caros (DACs de muy alta velocidad y CPUs), o no son de calidad para emisión en broadcast (como los que usan los IC monoliticos tipo BH1417, BA1404, etc), o muy inestables y difíciles de ajustar (MC1496), o no funcionan bien en todos los receptores FM (fallo de precisión en la subportadora de 38kHz).
De los que más me han gustado ha sido el de Pira.cz (http://pira.cz/eng/stk2en.htm), pero hay cosas que no me gustan de él. Lo que menos me gusta es la desviación de la portadora de 38kHz de unas cuantas decenas de hercios por no usar un cristal que sea múltiplo exacto de dicha frecuencia, que puede que para la mayoría de receptores funcione aceptablemente bien, pero para algunos falle la decodificación, en especial en los receptores baratos tipo SDR (algunos sólo sincronizan la fase de la piloto pero no ajustan la frecuencia sino que sintetizan directamente mediante FFT la portadora de 38.000kHz), que cada día son más comunes de encontrar en teléfonos móviles, aparatos de mp3/mp4, etc. Además pienso que el de Pira desperdicia recursos aunque obtiene buenas prestaciones. Pienso que es posible hacer algo de la misma calidad con elementos más sencillos (por ejemplo un MCU más económico)
De los basados en la multiplexación directa usando una cuadrada de 38kHz y dos switches tipo 4066 casi no hablo ya que padecen de todos los males, mucho fondo de ruido a causa de la cantidad de armónicos en la conmutación que no pueden terminar de filtrarse al estar muy cercanos a la banda pasante y una separación de canales muy pobre, alrededor de unos 15-20dB debido a la falta de compensación de niveles y falta de ajuste de la fase de la piloto, una vez senoidificada, con respecto a la subportadora.
Así que el primer objetivo es hacer un codificador económico, lo más preciso posible (como mucho 10Hz/20Hz de desviación con respecto a la portadora de 38kHz, y si es menor pues mucho mejor, ya que por encima de los 20Hz de desviación en algunos receptores se produce un efecto cacofónico familiar a aquellos que tienen receptores SSB). Deseable que tenga buen margen SNR, de 60dB si es posible, y una separación de canales acorde al SNR. Si tienes un margen SNR de 60dB no vale la pena conseguir una separación de canales mayor a 60dB ya que todo lo que quede por debajo de ese nivel quedará enmascarado por el ruido de fondo.
Esto obliga a utilizar un cristal de cuarzo que sea múltiplo entero de la portadora de 38kHz, de lo contrario estaríamos obligados de usar un PLL/Prescaler/Divisor de ratio de frecuencias, etc, y eso encarece mucho el proyecto. Además antiguamente era difícil conseguir cristales exactos pero hoy día con Internet y por el hecho de que los sistemas baratos también los usan, no es tan difícil conseguirlos.
De hecho este es un proyecto de diseño que tenía aparcado hace tiempo y que ha revivido gracias a que por casualidad hace unas semanas me encontré con una oferta de cristales 4.864MHz muy interesante y los acabé comprando. Con ellos he empezado a hacer mis primeras pruebas.
Estos cristales por lo que tengo entendido son muy difíciles de conseguir pero dan la ventaja de proporcionar un múltiplo de 38kHz que es exactamente una potencia de 2, es decir 128*38kHz = 4.864MHz. Lo que significa que dividiendo por 2^7 la frecuencia del cristal obtenemos la frecuencia de la portadora, y dividiendo por 2^8 tenemos la frecuencia piloto.
También he conseguido cristales de 4.332MHz. Esta frecuencia no es un múltiplo que solo contenga potencias de dos, pero tiene algo muy interesante… Contiene una potencia de 3 de 19kHz, lo que permite conseguir la portadora de 57kHz para el RDS además de la de 38kHz y la piloto de 19kHz.
Resumiendo, con el cristal de 4.864MHz se facilita el diseño de un codificador estéreo aunque se complica ligeramente la construcción del RDS (al no ser el cristal múltiplo de 3). Sin embargo con el de 4.332MHz se complica ligeramente el codificador estereo pero la portadora para RDS se obtiene fácilmente.
Además estoy a la espera de que me lleguen cristales de 38kHz y de 7.600MHz. Estos cristales aunque con ciertos inconvenientes, también son múltiplos enteros de 38kHz (1*38=38 y 200*38=7600) y usando algunas ideas pueden implementar codificadores de mayor calidad que para los que se usan tanto (estos cristales son bastante comunes de encontrar cuando se busca un poco por Internet, ya que son los que se usan para los codificadores monolíticos BA1404 (38kHz) y BH1417 (7.6MHz)).
Resumiendo. Lo diseños deberían estar orientados en utilizar uno de estos cuatro cristales (si encontráis otro posible cristal de una frecuencia múltiplo de 38kHz y que sea accesible de conseguir decidlo porque yo no lo he encontrado):
7.600MHz (Muy accesible y barato, estéreo no trivial, RDS no trivial).
4.864MHz (Raro, estéreo trivial, RDS no trivial).
4.332MHz (Menos raro, estéreo no trivial, RDS trivial).
38kHz (Relativamente accesible, no es caro, estéreo no trivial, RDS no trivial)
Bueno, yo he comenzado haciendo pruebas con el de 4.864MHz aunque he generado también una portadora estable de 38.000KHz usando el de 4.332MHz. Cuando me lleguen los otros cristales haré pruebas con ellos.
Comenzamos con la teoria:
Para aquellos que todavía no tengan claro cómo construir matemáticamente una señal MPX para FM a partir de dos canales de audio, no me voy a extender mucho ya que en estos enlaces lo explica mejor de lo que puedo explicarlo yo…
http://es.wikipedia.org/wiki/FM_estéreo
http://transmitters.tripod.com/stereo.htm
Pero voy a resumir toda la teoría anterior en la típica fórmula para obtener la señal multiplex:
MPX= (Vi+Vd) + (Vi-Vd) * S(38kHz) + 0,1 * P(19kHz)
Donde S es la subportadora senoidal de 38kHz y P la señal piloto de 19kHz. Vi es la señal de audio de canal izquierdo y Vd es la señal de audio del canal derecho.
La señal piloto no interviene en el proceso de codificación sino que se añade al 10% con el fin de servir para sincronizar la subportadora estereo. Así que para simplificar pondremos la señal MPX como :
MPX= (Vi+Vd) + (Vi-Vd) * S = A+B * S
En el receptor, se demodula B=(Vi-Vd) y se filtra A=(Vi+Vd) de esa forma se obtienen dos canales por separado, uno suma (A) y otro resta (B). De hecho el canal Vi se recupera sumando ambas señales (se cancela Vd), obteniendo 2*Vi, y el canal Vd se recupera restando ambas señales (se cancela Vi), obteniendo 2*Vd.
De cómo de balanceados se encuentren los niveles de A=(Vi+Vd) con respecto a B=(Vi-Vd), tanto en amplitud como en fase, dependerá la separación de canales. Esto significa que si por ejemplo el Vi de A no es el mismo exactamente que el Vi de B, en el receptor no se podrá cancelar Vi por completo al restar B de A y por lo tanto en el canal Vd aparecerá una parte del canal Vi, y viceversa, haciendo que la separación entre canales se resienta.
Por lo tanto, para un buen codificador estéreo necesitamos tres cosas:
-Hacer que los niveles Vi y Vd de la señal A sean los mismos que los niveles Vi y Vd de la señal B.
-Hacer que la señal piloto de 19kHz esté exactamente en fase con la de 38kHz.
-Que las condiciones anteriores no varíen con las condiciones de funcionamiento, temperatura, humedad, etc.
Mediante un codificador casi analógico, usando operacionales para generar las señales suma A (Vi+Vd) y resta B (Vi-Vd), y luego utilizar un modulador balanceado para conseguir una multiplicación en cuatro cuadrantes (es decir tanto voltajes negativos como positivos) como el MC1496 para generar la señal B*S, se consigue una separación muy elevada. Lamentablemente las condiciones de estabilidad duran poco ya que al variar los valores de los componentes con el régimen de funcionamiento enseguida sufre la separación de canales, lo que obliga a reajustar de nuevo las condiciones de funcionamiento.
La señal MPX de la fórmula anterior la podemos componer de forma equivalente de esta otra manera:
MPX = Vi * (1 + S) + Vd * (1 – S)
El paso de una fórmula a la otra es muy sencillo matemáticamente ya que sólo hay que operar con un poco de álgebra y recordar propiedades de la suma y la multiplicación.
Parece que ahora la forma de genera la señal se ha complicado al aparecer dos multiplicaciones en lugar de una, pero lo que hay entre los paréntesis, gracias a que suman el 1, y la señal S es una senoidal (la señal S varía entre 1 y -1), nunca valdrá menos de 0, de hecho valdrá entre 0 y 2. Esto hace que los multiplicadores sean de dos cuadrantes en lugar de cuatro, lo que es más fácil de conseguir. Hay un momento en que MPX vale 2*Vi+0*Vd= 2*Vi y otro momento, 180 grados de desfase, o lo que es lo mismo para 38kHz, unos 13,16 us después, MPX será 0*Vi+2*Vd= 2*Vd.
Consideramos que la señal MPX está compuesta por dos subseñales, MPXd y MPXi, que serían:
MPXi = Vi * (1+S)
MPXd = Vd * (1-S)
Y entonces MPX=MPXi+MPXd+0,1*Piloto.
Esta otra forma de expresar la señal MPX sugiere que tanto el canal Vi como Vd se van alternando paulatinamente en el tiempo. Sin embargo en un determinado momento intermedio no se tiene sólo Vi o Vd sino una combinación de ellos.
Por ello se han utilizado técnicas semidigitales para crear las multiplicaciones de (1+S) y (1-S) para los Vi y Vd con el fin de lograr una aproximación de MPX. Digo aproximación porque estas técnicas tratan de conseguir una S que se parezca a una senoidal en mayor o menor medida, pero siempre habrá algo de diferencia entre la señal digital creada por el codificador y la señal senoidal pura S.
El enfoque para un modulador económico es el uso de una señal C en lugar de la S que en lugar de ser Senoidal se aproxima por una Cuadrada que oscila entre +1 y -1. De hecho la señal (1+C) es una señal que vale 2 entre 0º-180º grados y 0 entre 180º-360º. La señal (1-C) será una señal desfasada 180º con respecto a la anterior, por lo que vale 0 entre 0º-180º y 2 entre 180º-360º.
Ya que las señales MPXd y MPXi se generan de la misma forma, con la portadora de 38kHz desfasada 180º, podemos considerar sólo los aspectos de la generación de la señal MPXi (portadora del canal izquierdo) que serán recícprocos en la generación de la portadora del canal derecho, o MPXd.
La multiplicación Vi *(1+C) se consigue fácilmente haciendo que entre 0º-180º ese valor sea 2*Vi, y entre 180º y 360º ese valor sea 0. Con el canal Vd de manera recíproca, entre 0º-180º será 0 y entre 180º-360º será 2*Vd.
Sin embargo, cuando obtenemos MPXi = Vi * (1+C), ya que C es una onda cuadrada de amplitud 1, esta se compone por una serie de fourier de infinitos armónicos impares de senoidales S, que quedan de la siguiente forma:
MPXi = Vi * (1+ 4/PI*(S+1/3*S(3)+1/5*S(5)…)
Esto es algo que no se parece especialmente mucho a la forma original MPXi = Vi*(1+S).
Donde S(3), S(5),... son los armónicos impares de la fundamental que componen la portadora cuadrada.
Si no se eliminan por completo estos armónicos, en el receptor ocurre un fenómeno de aliasing haciendo que aparezcan tonos fantasmas y artefactos en la señal audible que no deberían estar ahí, por lo que el SNR se resiente muchísimo y la calidad del audio se degrada bastante.
Para ello, es necesario un filtro que no distorsione la fase de la banda pasante y sea tan abrupto para eliminar a partir del tercer armónico, o es decir, que deje pasar hasta los 53kHz sin modificar la fase, pero anule al máximo las frecuencias de 95kHz en adelante. Esto es muy difícil de realizar por lo que los codificadores estereo que usen una cuadrada para generar las señales MPXd y MPXi tienen que elegir entre un SNR pobre o una separación pobre, dependiendo si filtran con un filtro muy abrupto que distorsione la fase o con un filtro menos abrupto que distorsione menos la fase pero deje pasar una parte de los armónicos.
Para complicar el asunto más, imaginemos que mediante un filtro ideal que corta a los 53kHz, eliminamos los armónicos S(3), S(5),… En ese caso obtenemos una señal
MPXi = Vi * (1 + S *4/PI)
Lo que hay entre paréntesis debería oscilar senoidalmente entre 0 y 2, sin embargo como S vale como máximo 4/PI y como mínimo -4/PI, lo que hay entre paréntesis acaba valiendo un valor máximo de 2.273 y un valor mínimo de -0.273…
Es decir, que el momento en el que la señal Vi debería valer 0, vale -0.273. Esto implica que la señal compuesta, MPX el instante en el que debería estar sólo presente Vd, es decir, 0*Vi+2*Vd en realidad hay esto: -0.273*Vi+2.273*Vd. Lo que significa que un 12% del canal Vi interfiere en el canal Vd y por lo tanto la separación máxima que podemos conseguir eliminando todos los armónicos es de -20Log(0.12)= 18,41dB. Una separación muy pobre.
Para mejorar esta separación, da igual cuanto valga MPXi en su valor máximo (ya que podemos variar su valor con un control de ganancia, tenemos que hacer que en su valor mínimo sea 0. Para ello a la señal completa se añade esto:
MPX(final)=MPX(filtrada) + (4/PI-1)*(Vi+Vd) =>
MPXi = Vi * (4/PI + S * 4/PI )= Vi * (1+S) *4/PI
Ahora aunque está el factor 4/PI, lo importante es que la señal que varía, es decir, lo que hay entre el paréntesis, va entre 0 y 2 por lo que MPXi valdrá entre 0 y Vi*2*4/PI.
Esto se traduce en que si implementamos un multiplexor que alterne las señales Vd y Vi, a la salida de ese multiplexor se debe de sumar un 27’3% de la señal suma (Vd+Vi) y de esa forma aumentamos considerablemente la separación de canales. Tristemente casi ninguna implementación de este tipo que utiliza switches tipo 4066 añade esta compensación.
Aquí se muestra gráficamente lo que se ha explicado:

En la figura 1, se ve la señal Cuadrada que es la que se usa para multiplicar Vi, y la señal teórica S que tendría que variar entre 0 y 2. En la figura 2 se tiene la señal cuadrada original, y la señal senoidal REAL que resulta tras filtrar el tercer y sucesivos armónicos. Notar el pico negativo de dicha senoidal. En la figura 3 se nota la onda cuadrada compensada sumándo un nivel de 0,273 *Vi, y la onda senoidal resultante que en ningún caso acaba estando por debajo de cero.
Pero aunque podamos compensar los niveles de señal, tenemos el problema de encontrar un filtro que elimine completamente el tercer y sucesivos armónicos y deje intacta la fase de la banda pasante. Por ello lo que sustituya a la senoidal S en la ecuación, no puede ser una simple cuadrada sino tiene que ser algo más.
En mis diseños usaré varias ideas para sintetizar la señal S con un mínimo de calidad que permita utilizar un filtro no tan abrupto pero que respete la fase, y al mismo tiempo la compensación, si es que es necesaria, sea menor que en el caso de la onda cuadrada.
Lo más lógico es que no necesitemos eliminar el armónico S(3) porque en la onda que utilicemos ese armónico no exista. Podemos usar un sistema para cancelar el tercer armónico de la señal que usemos para imitar S. Pongamos que tenemos la onda cuadrada C que hemos usado antes. Ahora la hacemos pasar por un retardo que a su salida muestre la misma señal C pero con un desfase de 60º. El tercer armónico tendrá un desfase de 60*3=180º, es decir tendremos –S(3). Si ahora sumamos esta onda con la onda original, el tercer armónico de la onda resultante sera S(3)+(-S(3))=0. Esa misma onda la dividimos por 2 para recuperar los niveles originales. De esa manera tenemos una onda M (cuadrada modificada o senoidal modificada) que recordará a la cuadrada original, pero que carece del tercer harmónico. Además el proceso se puede repetir desplazando nuevamente primero por 36º y depués por 25,71º para anular el armónico 5 y 7. El armónico 9 se anuló al anular el tercer armónico ya que el armónico 9 es múltiplo de 3. Una cuadrada que se ha retardado 3 veces y se ha promediado otras tantas veces acaba siendo una onda que contiene sólo 9 niveles (suficiente para ser generado con un DAC de 4 bits) y su primer armónico es el número 11 (es decir, en 418kHz, ya muy alejado de la banda que nos interesa y por lo tanto fácilmente filtrable sin alterar la fase de la banda pasante).
Aunque la señal sólo tiene 9 niveles, una vez filtrados por completo los armónicos restantes, no tenemos una señal de resolución 4 bits. Tenemos una señal senoidal pura (que habrá que compensar ya que siempre que quedan armónicos hay que compensar algo pero muchísimo menos que con la cuadrada original).
En la imagen siguiente se muestra el proceso de ir quitando armónicos promediando esa misma cuadrada con ella misma desfasada, y repitiendo varias veces para distintas fases…

De hecho este sistema de eliminación de armónicos por interferencias se le conoce como filtro peine (ya que no sólo elimina un armónico si no que todos sus múltiplos, haciendo ver que la respuesta del filtro se parecer a un peine) y funciona con cualquier forma de onda de entrada.
A modo de ejemplo se incluyen ondas modificadas eliminando armónicos donde en lugar de una cuadrada tenemos una triangular, y una parabólica.


Pero tomemos otra vez la onda modificada a partir de la cuadrada (que es más fácil de multiplicar que la triangular o la parabólica ya que la cuadrada sólo tiene dos estados).
Ahora supongamos que implementamos una cuadrada de 38kHz y la desfasamos 60º. Esas dos señales las usamos para multiplicar Vi de forma que generamos la siguiente expresión:
MPXi=Vi * (1+M)
Donde M ahora es 2*sqrt(3)/PI* (S+1/5*S(5)+1/7*S(7)…). Ahora vemos que ya no existe S(3) y los armónicos comienzan en S(5) que es el de 38*5=190kHz. Ahora ya es mucho más fácil filtrar esos armónicos ya que podemos usar un filtro que no sea tan abrupto y conserve mejor la fase. Si ahora filtramos, tenemos que nos queda el factor 2*sqrt(3)/PI =1,103:
MPXi=Vi * (1 + S * 1,103), es decir, que sin compensar hemos disminuido el crosstalk de un 12% a un 4,9% lo que da una separación de 26,3dB. No es un gran logro, pero son 8dB más que con la onda cuadrada. Además sólo hay que compensar con un 10.3% de la señal suma en lugar del 27,3% del caso de la onda cuadrada.
En la imagen siguiente se ven las figuras de antes pero ahora aplicadas a una onda modificada para eliminar el tercer armónico

Lo ideal sería poder implementar varios filtros con varios desfases para poder anular hasta el armónico 7, como se ha mostrado en las imágenes de más arriba, pero de forma analógica cuantos más desfasadores más fácil que alguno se vaya de fase por lo que acabamos teniendo otra vez niveles de armónicos que no filtra el filtro de salida. Sin embargo podemos utilizar un sobremuestreo digital para generar la señal senoidal exacta sin armónicos hasta el número 11. Esto requiere que la frecuencia de conteo sea un múltiplo de dichos armónicos para que al dividir por esas cantidades la frecuencia sea exacta, es decir, la frecuencia original tiene que ser múltiplo de 3, de 5 y de 7, lo que hace que deba valer x105. Lamentablemente no podemos conseguir el cristal necesario para poder alcanzar un sobremuestreo de x105, ya que el valor del cristal debería ser de 3.990Mhz. Alguien podría pensar que se podría usar un cristal de 4MHz y santas pascuas, ya que casi casi se llega a tener a 4MHz pero al dividir por 105, la frecuencia resultante sería de 38,095kHz, lejos de nuestra pretensión de conseguir los 38,000kHz exactos.
Sin embargo si sólo queremos eliminar “digitalmente” el armónico tercero ya que disponemos de un filtro decente para eliminar el quinto y sucesivos, lo podemos hacer relativamente fácil utilizando un cristal de 4.332kHz (ya que es múltiplo de 3), disponible fácilmente y de paso ya obtener la señal de 57kHz para alimentar un enconder RDS.
Aquí os propongo dos sistemas para lograr codificar mediante una onda modificada para elimnar el tercer armónico. El primero genera una cuadrada a 38kHz mediante un cristal de esa frecuencia, y una red de desfase genera una señal desfasada 60º (el desfasador puede ser una red RC que retrase la cuadrada durante 4,4 us y un trigger schmitt que vuelva a conformar la señal en cuadrada. Entonces usamos ambas señales para combinarlas en un sumador obteniendo la multiplicación directa de ambos canales por las señales (1+M) y (1-M). Los restantes bloques no necesitan mucha explicación. Está la red de compensación para anular el crosstalk, y el sistema para generar la señal piloto de 19khz mediante un biestable tipo T y un conformador de onda senoidal (puede ser un filtro en 19kHz con una Q bastante elevada), además de otro retardo para poder ajustar la fase senoidal para minimizar de nuevo el crosstalk.

El segundo sistema hace lo mismo que el primero pero las señales desfasadas son generadas por un contador secuencial de 6 estados. Este sistema tiene la ventaja de que por diseño el desfase de 60º no puede variar por las condiciones de funcionamiento, frio, calor, humedad, etc. Por lo demás es igual que el primero, aunque este usa un cristal de 4.332MHz y permite generar además la portadora RDS de 57kHz.

Otro método para multiplexar con una senoidal:
Además de la cancelación de armónicos, es posible sintetizar las señales (1+S) y (1-S) mediante otros métodos. El más utilizado en codificadores con sobremuestreo es el uso de DACs multiplicadores de dos cuadrantes o bien un DAC multiplexado a distintos niveles. El DAC típico es aquel que hace uso de una matriz de resistencias para proporcionar a su salida el nivel analógico proporcional a la señal digital de entrada. Los más conocidos de este tipo son las redes R-2R en escalera, y las resistencias ponderadas (cuando se pretende generar señales periódicas conocidas).
Otro tipo de DACs menos conocidos pero más comunes ya que funcionan casi enteramente en el terreno digital, son los DACs con modulación por densidad de pulso o PDM. No confundir con PWM o modulación por ancho de pulso, que se trata de otra forma de implementar un DAC pero no tan digital… A la modulación PDM también se la conoce por su construcción, como modulación Delta-Sigma (o Sigma-Delta). Un modulador Delta-Sigma lo que hace es rastrear una señal analógica generando pulsos más “juntos” cuanto más alto sea el nivel de la señal analógica. Para una descripción más detallada visitad el enlace de la wikipedia sobre esta modulación:
http://es.wikipedia.org/wiki/Modulación_Sigma-Delta
Una característica de este sistema es que para alcanzar una buena resolución es suficiente con pocos bits siempre que podamos hacer funcionar el modulador mucho más rápido que la frecuencia que queremos sintetizar. De hecho es bastante común ver moduladores Sigma-Delta utilizando solamente un bit.
La característica de este modulador se basa en que los armónicos en lugar de ir desplazándose por igual a lo largo del espectro, se concentran en la parte alta de él, por lo que un sencillo filtro pasa bajo con la frecuencia de corte alejada de la zona donde la densidad de armónicos es mayor, reconstruye fielmente la señal original.
Nosotros no necesitamos la parte ADC, es decir, el rastreador que genera los bits. Podemos generar una tabla de bits que contengan la secuencia Delta-Sigma de una senoidal a una determinada frecuencia, y esa tabla guardarla en una memoria rápida, ya sea una EPROM, una RAM, o un microcontrolador. Sin embargo la parte DAC del modulador, puede ser tan sencilla como un filtro RC con la frecuencia de corte dos décadas por debajo de la frecuencia de muestreo (consiguiendo 40dB de atenuación de los armónicos molestos). Es decir, un simple switch conmutando rápidamente pongamos a 128 veces la frecuencia que se quiere sintetizar, y luego al filtrar obtenemos el canal de audio correspondiente multiplicado con la senoidal (1+S) con una resolución bastante aceptable.
La siguiente imagen muestra las ondas cuando la frecuencia del chorro de bits es de 128 veces la frecuencia de la subportadora, es decir 128*38=4.684MHz. Además fácilmente podemos generar varias ondas a la vez ya que disponemos de varios bits en la memoria por cada posición temporal de la secuencia. Por ejemplo podemos utilizar 1 o dos bits tanto para generar las ondas de 38kHz como la piloto de 19kHz.

Los siguientes esquemas se basan en este principio. El primero usa una memoria tipo EPROM y un cristal que alimenta el reloj del contador que direcciona dicha memoria. Para generar la señal de 19kHz es necesario repetir 2 veces la de 38kHz, por lo que con un cristal de 4.864MHz hace falta 256Bytes, con uno de 7.6MHz, 400Bytes, y con el de 4.332MHz, 228Bytes. Excepto en el caso del cristal de 4.864MHz, para los otros cristales la posición siguiente a la última de la tabla hace que el contador se resetee y vuelva al principio de la memoria.


Aunque en estos esquemas no aparece, al eliminar una buena parte de los armónicos, el nivel de la onda fundamental se reduce notablemente, pero no así el nivel de continua. Esto significa que es necesario compensar aunque en este caso en lugar de sumar a MPX la señal (Vi+Vd) hay que restar un tanto por ciento de ella, equivalente al nivel excedente de dicha señal en la señal compuesta final.
Pruebas en protoboard
Para tratar de generar tanto los pulsos a 38kHz y 19kHz como las ondas senoidales correspondientes a esas frecuencias, he probado de momento utilizando la tabla de ondas Delta-Sigma que he generado para construir la gráfica que hemos visto anteriormente. He usado dos bits para codificar la señal de 38kHz PDM de 2 bits, un bit más para codificar la misma señal con resolución de 1 bit, y 3 bits más para generar las de 19kHz de dos bits y la de 1 bit. En total he usado 6 bits de los 8 disponibles en una memoria paralela EEPROM modelo X2804 de Xicor (es lo que tenía por el cajón desastre). Como no son muchos bytes la he programado manualmente.
He usado un cristal de 4.864MHz con una puerta 74HC04 para generar el tren de ondas que alimenta al contador.
Precisamente el problema de mi montaje y el que me ha limitado bastante los resultados ha sido utilizar una versión de baja velocidad del 4040, como es el MC14040 que funciona bien hasta los 2MHz para 5V (le he dado un tren de pulsos de más del doble de rápido). El contador contaba, pero Q1, es decir A0 en la memoria, nunca bajaba de 2,5V por lo que siempre quedaba en 1. El resultado es que con este contador sólo he podido direccional las direcciones impares de la memoria a esa velocidad por lo que el sobremuestreo se reduce de x128 a x64. Además la falta de velocidad hace que las direcciones se arrastren en la serie (van retrasadas con respecto al tren de pulso) lo que hace que la onda resultante no sea perfectamente senoidal sino que se arrastra ligeramente hacia atrás.
Espero corregir estos problemas cuando consiga un 74HC4040 que es 10 veces más rápido que el MC14040.
De momento estas son las imágenes que he ido obteniendo de las pruebas. Aquí muestro una imagen de la parte generadora Delta-Sigma montada en protoboard:

Aquí una foto de la onda cuadrada generada por el cristal:

En la siguiente foto, la salida Q8 del contador (19,000 kHz es decir 4864/256)

En la siguiente foto, la salida Q7 (38,000 kHz es decir 4864/128)

En la siguiente foto, se tiene la señal PDM de 19,000KHz de un bit con respecto al reloj de 19KHz.

En la siguiente foto, se tiene la señal PDM de 38,000KHz de un bit con respecto al reloj de 38KHz.

En la siguiente foto, coloqué un pasabaja RC con una resistencia de 10k y un condensador de 470pF a la salida de cada una de las señales PDM, de 19 y 38kHz. La señal de 19kHz se reconstruye bastante bien a pesar de ser solo de 1 bit, aunque la asimetría se debe al arrastre de bits que he comentado antes por culpa del contador. Sin embargo aunque también debería convertirse bien, la señal PDM de 38kHz aparece formada como si fuera una triangular.

Ya en la última foto, el arrastre de bits para la señal PDM de 19kHz y dos bits de resolución no la puse ya que aunque mejoraba la simetría, una zona presentaba una fuerte distorsión. Sin embargo la de 38kHz si que mejoraba al usar 2 bits (básicamente colocar 2 resistencias de 10k en las dos salidas y unidas en el mismo condensador de 470pF que hace de integrador y sumador de ambas señales). Ahora ya en la de 38kHz se ve sintetizada claramente senoidal.

De momento estas son las pruebas que he hecho. Quiero conseguir más integrados lógicos, como más contadores, flip-flops, más puertas rápidas, etc. Así podré implementar varias versiones de los diseños que he mostrado y ver cual de todos es más estable, genera menos ruido, más separación, es amigable con el RDS, etc.
De ahí el título de este POST. Soy una persona de recursos limitados, y además me gustaría que este proyecto fuera colaborativo y quedara como diseño del foro (luego ya cada uno que hiciera lo que quisiera con él).
Propuesta:
Por ello me gustaría saber si hay gente dispuesta a probar las ideas que he explicado aquí, en definitiva contribuir a concretar algunos de los diseños que he propuesto, ya sea materializando los bloques funcionales o añadiendo más (filtros de pre-énfasis, etc). Y una vez tengamos unos cuantos moduladores estéreo, diseñar el modulador RDS que mejor se adapte al modulador estéreo (usando la frecuencia de reloj maestra por ejemplo).
No es un proyecto que tenga que hacerse rápido, es decir, que me da igual si cuesta un año o más en realizarse, pero si sale algo decente podríamos tener un diseño que se hiciera popular y así dar algo de publicidad al foro.
Como sale más barato comprar cantidad de componentes cuando compras por ebay y otros sitios online, tengo más cristales de los que voy a utilizar.
Dispondría para compartir los siguientes cristales que son difíciles de conseguir, en principio para compartir 1 cristal por persona:
10 cristales de 4.864MHz.
10 cristales de 4.332MHz.
Y en cuanto me lleguen por correo compartiré además los siguientes:
10 cristales de 7.600MHz.
10 cristales de 38kHz.
No cobraría nada por el cristal, lo único que pido sería los gastos de envío que para España sería de 1 euro aproximadamente, y se haría mediante correo ordinario. Para fuera de España en especial para Latinoamérica el envío se multiplica varias veces por lo que en un principio lo ideal sería que participaran foreros españoles, aunque alguien que consiga los cristales por su cuenta o esté dispuesto a pagar los gastos de envio internacionales, bienvenido sea.
Además si alguien necesita más de un cristal, tendría que justificarme por qué quiere más de uno. Tiene que ser también alguien del foro, es decir, alguien que participe activamente. Aunque no tenga muchos mensajes, tiene que tener al menos mensajes que sean relevantes o algún que otro aporte.
Los interesados en un cristal que comenten que quieren participar en el diseño en este mismo hilo.
El diseño debería de comenzarse a concretar o implementar, o por lo menos alguna de sus partes, antes de 6 meses desde la fecha en que envíe el cristal. No importa que después se tarde en terminar el proyecto, lo importante es que al menos empiece.
Bueno, pues espero vuestras ideas y aportes al proyecto, y como no, vuestras solicitudes.
Ahh, si alguien quiere implementar el proyecto utilizando una tabla generada en una memoria RAM de alta velocidad, dispongo de 10 chips de RAM estática HM6116 reciclados de una máquina recreativa. Podría enviar uno de ellos junto al cristal (siempre que el sobre en total no supere los 20 gramos).
Un saludo, y gracias por llegar a leer hasta el final.
Última edición: