Follow along with the video below to see how to install our site as a web app on your home screen.

Nota: This feature currently requires accessing the site using the built-in Safari browser.
No, de los artículos que he leido (unos pocos) no daban detalles del método de cálculo.Eduardo, tenes bibliografia sobre este tema?
Dos sensores y una diferencia de tiempo te definen una hipérbola.Resolviste el problema con una ecuacion, sin saber el tiempo de emision? No puede ser, son tres incognitas independientes... necesitasvtres ecuaciones.
% This simulation makes positioning inside a rectangle
% There are sensors in three corners of the rectangle
% and an object inside emits sounds to the sensors
Len = 180;
Heigth = 100;
% Positions of the sensors in cm
x = [0, 0, Len];
y = [0, Heigth, 0];
% Resolution of the positioning table in cm
res = 4;
% Speed of sound in cm/ms
vs = 34.02;
% time of emission of a pulse from the sensor - it is not needed,
% the calculation cancels it, but several values can be tested to see
% that it doesn't affect the results
ts = 15; % in ms
% matrix of delta distance for each position of the emitter
Xt = linspace(res/2, Len-res/2, Len/res);
Yt = linspace(res/2, Heigth-res/2, Heigth/res);
for ii = 1:size(Xt)(2)
for jj = 1:size(Yt)(2)
% calculate time of arrival of signal to each sensor
t = sqrt( (Xt(ii)-x).^2 + (Yt(jj)-y).^2 ) / vs + ts; % in ms
d21(ii,jj) = t(2)-t(1);
d31(ii,jj) = t(3)-t(1);
end
end
accum_err = 0;
% Now detect several positions
for tt = 1: 100
% generate sensor data
xpi = rand*Len;
ypi = rand*Heigth;
ts = 10 + rand*30;
% measured values
ta = sqrt( (xpi-x).^2 + (ypi-y).^2 ) / vs + ts ; % in ms
d21a = ta(2)-ta(1);
d31a = ta(3)-ta(1);
% explore the table and calculate quadratic error
err = 10000;
ia = 1; % index to the distance tables
ja = 1;
for ii = 1:size(Xt)(2)
for jj = 1:size(Yt)(2)
err_new = (d21a-d21(ii,jj))^2 + (d31a-d31(ii,jj))^2;
% Lower error found, candidate for estimated position
if (err_new < err)
err = err_new;
ia = ii;
ja = jj;
end
end
end
% To show maximum quadratic error
xpa = res * (ia-0.5);
ypa = res * (ja-0.5);
new_accum_err = (xpi-xpa)^2+(ypi-ypa)^2;
if (new_accum_err > accum_err)
accum_err = new_accum_err;
xpam = xpa;
ypam = ypa;
xpim = xpi;
ypim = ypi;
end;
end;
printf('Maximum quadratic error after 100 tests - Real x position: %g, estimated x position: %g\n', xpim, xpam);
printf('Real y position: %g, estimated y position: %g\n\n\n', ypim, ypam);También probé de seguir reemplazando algebraicamente para obtener la expresión de Y a partir de los datos, y llegué a esto:A = 182.587;
B = 229.1;
D = 668.689;
L1=1800;
L2=1000;
H = L1/2;
V = L2/2;
M1 = (V/H) *(D-B)/A;
B1 = (D-B) *(D+B-A)/(4*H);
M2 = (V/H) *(2*D-A)/A;
B2 = (V*V-H*H+D*D-D*A)/(2*H);
X = (B1*M2 - B2*M1)/(M2-M1)
Y = (B1 - B2)/(M2-M1)
que da el resultado con la misma precisión de la fórmula anterior.A = 182.587;
B = 229.1;
D = 668.689;
L1=1800;
L2=1000;
H = L1/2;
V = L2/2;
Y = ((D-B)/2 - (V*V - H*H + D*(D-A))
Y =Y /(D+B-A))
Y =Y *A/(2*V)
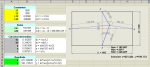
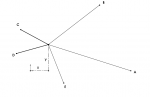
% Coordenadas de los sensores
A = [ 325.41377769 , 0 ] ;
B = [ 224.33606904 , 211.33832358 ] ;
C = [ -31.3004399 , 132.49461234 ] ;
D = [ -45.0387352 , 55.55330358 ] ;
E = [ 108.13874084 , -39.60976031 ] ;
u = ones(5,1); v = [1 1 -1]; % Matrices auxiliares
% Tiempo leido en cada sensor
% Como es un test, arbitrariamente le reste 100
% a las distancias originales
ta = 179.81796019 ;
tb = 108.88095227 ;
tc = 2.01302202 ;
td = 7.51169039 ;
te = 33.39535394 ;
Ti = [ta;tb;tc;td;te] ; % Matriz de tiempos leidos
%-------------------------------------------------------
% Resolucion
P = [[A;B;C;D;E],Ti] ; % Armo la matriz principal
Pm = mean(P) ; % Matriz con el promedio de la posicion y los tiempos
Pc = P-u*Pm ; % Traslacion de coordenadas
B = Pc.^2*v' ; % Matriz con xi^2 + yi^2 - ti^2
Bm = mean(B) ; % Su promedio
Bc = B - u*Bm ; % Sus valores respecto del promedio.
Xc = Pc\Bc/2 ; % Resuelve el sistema por LMS
X = Xc' +v.*Pm % Traslado para obtener [x,y,T+tm]
Tabs = Ti + u*X(3) % Tiempos de transito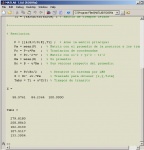
Por lo visto últimamente has andado mucho por el baño. Te recomiendo comer un poco de queso de rallar.El resto es álgebra en el baño.
Esto puede no ser tan fácil de implementar en general, porque por razones de construcción del resto del sistema (las esquinas de una pantalla, o de una habitación, etc.) uno puede verse obligado a ubicar los sensores más o menos regularmente.Algo que no es problema, pues fácilmente se pueden ubicar los sensores de tal manera que nunca los tiempos de todos sean parecidos.
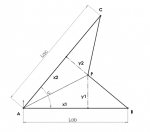
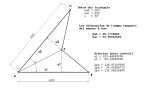
%----------------------------
% Datos
Lab = 200 ;
Lac = 230 ;
u = 50 ;
d1 = 39.7776862 ;
d2 = 23.30912496 ;
%----------------------------d1 = d1/Lab ; % diferencias relativas
d2 = d2/Lac ;
p = Lab*(1-d1^2) ;
q = Lac*(1-d2^2) ;
se = sin(u*pi/180) ;
co = cos(u*pi/180) ;
% Calcula los coef. y resuelve
% la ec. de 2do grado
a = se^2 + 2*co*d1*d2 - d1^2 - d2^2 ;
b = p*(d1-co*d2) + q*(d2-co*d1) ;
c = p^2 + q^2 - 2*p*q*co ;
t = (b+sqrt(b^2+a*c))/a ;
% Coord. x1
x1 = Lab*(1+(t/Lab-d1)*d1)/2
% En Matlab, evaluar y1 de esta forma
% no tiene ninguna ventaja numerica,
% pero si se trabajara con precision
% simple (float) si.
x2 = Lac*(1+(t/Lac-d2)*d2)/2 ;
y1 = (x2-x1*co)/se
Raíz(x):
- Escoja dos números
y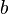 tales que
tales que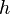
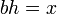
- Si
vaya al paso 6, si no, vaya al paso 3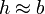
- Asigne
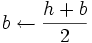
- Asigne
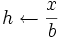
- Vaya al paso 2
- Escriba "
"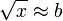
Bueno... el tipo de datos, el hardware y el objetivo del cálculo son quienes deciden el algoritmo a utilizar....La causa por la que me "emperre" en conseguir ecuaciones lineales es porque me parece que son mucho mas faciles de resolver que ecuaciones que contienen senos y cosenos, sobre todo si hipoteticamente lo hicieramos en un micro.
function [X,w] = Posicion(Xs,Ws)
% Xs : Matriz con las coordenadas de los sensores
% W : Matriz con los tiempos leídos en cada sensor
% X : Matriz con la posicion [x y] o [x y z]
% w : Instante en que se emitió el pulso
% Traslado de coordenadas al baricentro
Xm = mean(Xs) ;
wm = mean(Ws) ;
Xc = Xs-ones(length(Xs),1)*Xm ;
Wc = Ws-wm ;
% Evaluacion de las matrices Xo y M
% aplicando la pseudoinversa
B2 = sum(Xc.^2,2)-Wc.^2 ;
bm = mean(B2) ;
Xo = Xc\B2/2 ;
M = Xc\Wc ;
% Evaluacion de los coeficientes
% de la ecuacion de 2do grado
a = 1-M'*M ;
b = Xo'*M ;
c = Xo'*Xo + bm ;
w = (b-sqrt(b^2+a*c))/a ;
% Restauracion de coordenadas
X = Xm + Xo' + M'*w ; % Coordenadas del movil
w = wm + w ; % Instante de emisionfunction W = Tiempos(Xs,X,we)
% Xs : Matriz con las coordenadas de los sensores
% X : Matriz con la posicion [x y] o [x y z]
% we : Instante de emisión del pulso
% W : Matriz con los tiempos leídos en cada sensor
W = sqrt(sum((Xs-ones(length(Xs),1)*X).^2,2)) + we ;% Coordenadas xyz de los sensores
% Para 3D la cantidad mínima son 4
A = [ 1000 -1000 1000 ;
1000 900 1200 ;
-700 700 700 ;
700 700 100 ;
300 0 100 ;
100 100 -700 ;
-600 -900 800 ];
% Coordenadas del emisor
X = [ -10 300 45] ;
% Genero los tiempos que se leeran para un
% instante emisión en we = 400
W = Tiempos(A,X,400) ;
% Obtengo la posición correspondiente
% a esos tiempos.
% Debe darme lo que puse al principio
% X=[-10 300 45] y we=400 :)
[X2,we] = Posicion(A,W)El problema de usar Matlab es que hay cosas que hace que no te dice cómo las hace.
Entonces, para pasar eso a un micro ...
Vos acá no usas nada raro, salvo la operación " \ ", que para pocas variables (< 30)
puede reemplazarse por el método de Gauss-Jordan.
(Comento esto, pero no me puse a controlar demasiado e fondo el método propuesto. )

